役に立つ薬の情報〜専門薬学＞統計学＞二標本t検定
役に立つ薬の情報〜専門薬学 サイトマップ


　　　二標本t検定
　独立2群の差の検定
関連2群と独立2群の違いであるが、「同じ個体」で調べるか「違う個体」で調べるかの違いである。前者が関連2群で後者が独立2群である。

同じ個体なら、例えば薬を投与する前と後での変化を見ることができる。しかし、異なる個体でペアを組んで、その前後で変化を見るのはダメである。なぜなら、全く違う個体の変化だからである。

そのため、異なる個体でのデータである独立2群は二つの群の平均値を比べるのである。

　　　


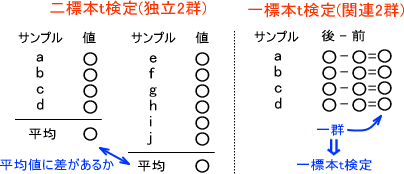
　二標本t検定(パラメトリック法)
二標本t検定の条件として次の二つがある。
・正規分布している
・等分散している

等分散しているかどうかはF検定によって確かめることができる。

・仮説の設定
帰無仮説(H0)：「2群間に差がない」と仮定する。
対立仮説(H1)：「2群間に差がある」と仮定する。

・確率を求める
正規分布しており、等分散していると分かったとする。このときの検定は二標本t検定を使い、二標本t検定でt値を出すにはそれぞれ両群の「平均値x、分散s2」を計算して求める必要がある。

t値は下の式より求めることができる。

　

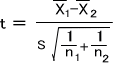
このときのsは両群の分散s12,s22から合成した分散であり、下の式から求めることができる。


　

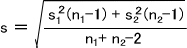
また、このときの自由度dfは n1+n2-2のt分布に従う。自由度dfを求めたらt分布表からtαを求めて、計算したt値と比較する。

・判定
｜t｜≦tαのとき、P≧αとなり帰無仮説を棄却できない。
｜t｜＞tαのとき、P＜αとなり帰無仮説を棄却する。有意差あり。

………………………………………………………………………………………………………………

　例題
Aクラスには7人、Bクラスには9人の生徒がいる。この生徒たちに物理のテストを実施した。AクラスとBクラスの物理のテストの実力はどちらかのクラスの方が優勢であるといえるかどうか検定しなさい。なお、データは正規分布しているとする。

Aクラス
49
40
52
37
55
38
45
Bクラス
60
52
68
55
65
47
45
62
53
(注：このデータは便宜的に作ったもので、実際のデータではない)

帰無仮説(H0)：AクラスもBクラスも物理のテストの実力に差はない。
対立仮説(H1)：AクラスとBクラスには物理のテストの実力に差がある。

・計算
この例題はF検定で出した時と全く同じ問題であり、F検定のときの計算よりこのデータは「等分散である」といえる。つまり、このデータは「正規分布」と「等分散」の両方の条件を満たしているので二標本t検定を使うことができる。

上の2群のデータからデータ数n、平均値x、標準偏差s、分散s2をまとめると下のようになる。

Aクラス Bクラス
データ数n 7 9
平均値x 46.3 56.3
標準偏差s 8.65 7.94
分散s2 74.9 63

その次に合成した分散値sを出さなければならない。両群の分散から合成した分散を出すには、下のように計算する。

　

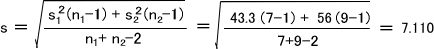
このデータからt値を計算すると下のようになる。

　

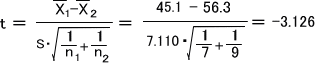
このとき、自由度df＝n1+n2-2＝7+9-2＝14のt分布に従うので、t分布表よりt0.05＝2.145であると分かる。

計算したt値＝2.405＞2.145＝t0.05より、t＞t0.05となるのでP＜0.05となる。よって、帰無仮説を棄却し対立仮説を採用するので、「AクラスとBクラスには物理のテストの実力に差がある」ということができる。

………………………………………………………………………………………………………………

　Welch法
F検定で等分散とみなせなかった場合、Welch法を使うことができる。計算の仕方は二標本t検定とほとんど同じで、t値と自由度dfを求める計算式が違うだけである。

下にWelch法でのt値と自由度dfを求める式を示す。

　

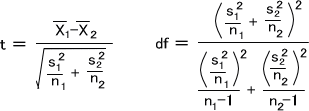
すごい計算式ですが、がんばって計算してください。