役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 統計学 ＞ F検定 (等分散の検定)

F検定 (等分散の検定)

 

　F検定(等分散の検定)
まず「等分散とは？」であるが、漢字を見て分けるとおり等しく分散しているということである。つまり、それぞれの群の分布の形が似ているということである。

 

下にいくつかの例を示す。

 

　

 

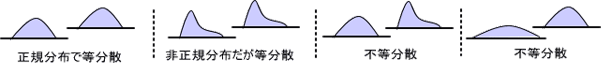
独立2群の差の検定の場合、二標本t検定には「正規分布である」「等分散である」の二つの条件が必要である。そのため、たとえ正規分布していても等分散でなければ二標本t検定を使ってはいけない。

 

この等分散かどうかを調べるためにF検定がある。二標本t検定をする前にF検定をして等分散であることを確認する必要がある。

 

もし、F検定で「等分散でない」と検定されたなら二標本t検定ではなくてWelch法やMann-Whitney検定で検定しなくてはならない。

 

・仮説の設定
帰無仮説(H₀)：「2群間の分散に差がない(等分散である)」と仮定する。
対立仮説(H₁)：「2群間の分散に差がある(等分散でない)」と仮定する。

 

・確率を求める
最初にそれぞれの群の分散s₁²,s₂²を求める。各群の分散を求めることができたなら、下の式によってF値を出す。ただし、分子に大きい数値の方をとる。

 

　

 

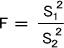
このとき、自由度は分子の自由度df₁＝n₁-1、分母の自由度df₂＝n₂-1のF分布に従う。自由度が求まったらF分布表からF_αを求めることができる。

 

・判定
1≦F≦F_αのとき、P＞0.05となる→帰無仮説を棄却できない→等分散である。
F＞F_αのとき、P＜0.05となる→帰無仮説を棄却する→不等分散である。

 

………………………………………………………………………………………………………………

 

　例題
Aクラスには9人、Bクラスには7人の生徒がいる。この生徒たちに物理のテストを実施した。AクラスとBクラスの物理のテストの点は等分散かどうかを検定せよ。

Aクラス 60 52 68 55 65 47 45 62 53

Bクラス 49 40 52 37 55 38 45

(注：このデータは便宜的に作ったもので、実際のデータではない)

 

帰無仮説(H₀)：2群間の分散に差がない(等分散である)
対立仮説(H₁)：2群間の分散に差がある(等分散でない)

 

・計算
まず、このデータのデータ数n、標準偏差、分散をまとめると下のようになる。

 

	Aクラス	Bクラス
データ数	9	7
標準偏差	7.48	6.58
分散	56	43.3

 

この分散の値からF値を求めるのだが、数値が大きい方を分子にするのでs_A²＝56の方を分子にする。F値を計算すると次のようになる。

 

　F ＝ 56/43.3 ＝ 1.29

 

このとき、F_0.05は分子の自由度df₁＝9-1＝8、分母の自由度df₂＝7-1＝6のF分布に従う。F分布表より、F_0.05＝4.15である。

 

F ＝ 1.29＜4.15 ＝ F_0.05なので、P＞0.05となり帰無仮説を棄却できない。「2群間の分散に差がある」とは言えないため、等分散とすることができる。