役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 物理化学 ＞ 複合反応・アレニウス式・拡散

複合反応・アレニウス式・拡散

 

　複合反応
複合反応とは、薬物がA→Pへと変化する単純な反応ではなく可逆反応や逐次反応などの複雑な反応を複合反応という。

 

さまざまな反応が合わさった複合反応で、その反応の速度を支配する段階を律速段階という。律速段階はその反応の中で一番遅い反応段階である。

 

例えば、「A→B→C→P」と変化するとき「B→C」の反応速度が一番遅いとする。このとき、複合反応の中で「B→C」へと変化する反応が律速段階である。一番遅い反応がどれだけの速度で起こるかで、その反応全体の速度が決定する。

 

・可逆反応
A→Pへと変化すると同時にP→Aと変化する反応が可逆反応である。可逆反応では、反応が完全に右に進行することはない。反応物と生成物が同じ割合で生成すると平衡状態となる。

 

　

 

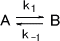
Aが反応してPを生成するときの速度定数をk₁、Pが反応してAを生成するときの速度定数をk_-1とする。それぞれの反応速度は次のように表わされる。

 

　v_B = k₁[A] 　←Bの生成する速度

 

　v_A = k_-1[B]　←Aの生成する速度

 

このとき、実際にPが生成する速度は次の式で表わされる。

 

　v = k₁[A] - k_-1[B]

 

平衡状態のとき、v_Aとv_Pそれぞれの反応速度は同じになるはずである。なお、平衡濃度をそれぞれ[A]_eq,[B]_eqで表す。

 

　v_A = v_P

 

　k₁[A]_eq = k_-1[B]_eq -①

 

　k₁[A] - k_-1[B] = 0

 

また、平衡定数Kは次の式によって求めることができる。

 

　

 

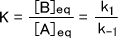
平衡定数は①式の両辺をそれぞれ[A]_eq,k_-1で割れば導き出せる。なお、可逆反応のときの反応物・生成物の百分率-反応時間曲線は次のように表わされる。

 

　

 

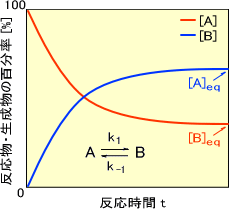
・並行反応(並発反応、競争反応、分岐反応)
一つの物質から複数の物質を生成するときの反応を並行反応という。この反応は並発反応や競争反応、分岐反応と言う場合もある。

 

下のようにAという物質がB,C,Dという物質を生成し、それぞれの速度定数がk_B,k_C,k_Dとする。

 

　

 

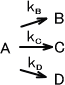
このとき、それぞれの生成速度は次のようになる。

 

　v_B = k_B[A]　、　v_C = k_C[A]　、　v_D = k_D[A]

 

また、反応物Aの減少速度は次の式に従う。なお、このときの速度定数kはk_B,k_C,k_Dの和となる。

 

　-v_A = k[A]　(k=k_B k_C k_D)

 

並行反応で生成物が二つの場合、濃度-反応時間曲線は次のように表わされる。

 

　

 

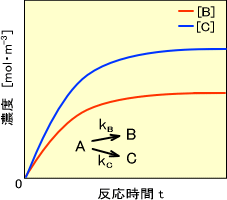
・逐次反応(連続反応)
反応物が中間生成物を介して最終生成物となる反応を逐次反応(連続反応)という。逐次反応の例としては次のような反応がある。

 

　

 

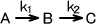
Aが反応物、Bが中間体、Cが生成物である。このとき、速度定数をそれぞれk₁,k₂とすると、生成速度(減少速度)は次のように表わされる。

 

　-v_A = k₁[A]　←Aの減少速度

 

　v_B = k₁[A] - k₂[B]　←Bの生成速度

 

　v_C = k₂[B]　←Cの生成速度

 

このときの濃度-反応時間曲線は次のように表わされる。

 

　

 

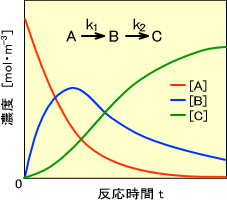
　アレニウス式(反応速度と温度)

 

反応速度と温度は密接に関係している。温度が上昇すると、反応速度も上がるのである。この関係を式として表したのがアレニウス式である。

 

物質同士が衝突して化学反応が起こり、新たな結合を形成することで新しい物質を生成する。つまり、化学反応の速度には衝突回数を規定する「頻度因子A」と反応を起こすのに必要なエネルギー(活性化エネルギーEa)に依存しているのである。

 

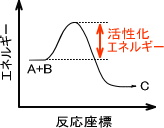
なお、頻度因子Aは前指数因子とも呼ばれ、定数である。

衝突回数が多ければそれだけ反応する分子の数が多いはずである。また、反応を起こすのに必要なエネルギーが小さいほど反応は起こりやすいはずである。

 

温度が上がれば運動エネルギーが上昇するので分子同士の衝突回数(衝突確率)が上昇する。そのため、温度が上がると反応速度が速くなるのである。

 

アレニウス式は次のように表わされる。なお、Aの単位はkと同じである。

 

　

 

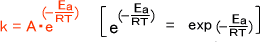
アレニウス式で両辺のlnを取ると下の式のようになる。

 

　

 

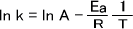
頻度因子A,気体定数Rは定数であり、活性化エネルギーEaも固有の値であるので、lnkの値は温度によって変化する。つまり、y=b-axの簡単な式と見ることができるのである。

 

温度(1/T)によってlnkの値をプロットしていくと直線のグラフを得ることができる。このときの傾きは-Ea/Rであり、切片はlnAである。つまり、このグラフから活性化エネルギーEaと頻度因子Aの値を求めることができるのである。このプロットをアレニウスプロットという。

 

　

 

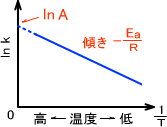
なお、活性化エネルギーが大きい物質ほど傾きが大きいので、温度依存性が高くなる。

 

※ミカエリス・メンテン式は「生化学Ⅰ」の「速度反応論」で述べているので省略する。

 

　拡散(フィックの第一法則)
ある溶液で濃度が濃い部分と淡い部分があるとする。当然ながら、この溶液は全体の濃度が均一になるように働き、xの方向(濃度が薄い部分)に向けて移動する。つまり、拡散するのである。

 

　

 

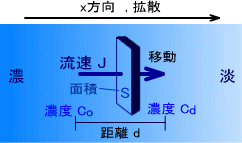
単位面積、単位時間当たりに通過する溶質の量を流束 (mol/m²・s)という。このとき、断面積Sを⊿t秒で動く溶質の量はJS⊿tで表わされる。

 

また、このとき通過する溶質の量は「濃度差とその距離による濃度勾配(Co-Cd)/d」、「断面積S」、「時間⊿t」に比例する。よって、次の式を導き出すことができる。

 

　

 

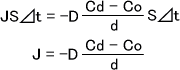
Dは比例定数であり、拡散係数と呼ばれている。

 

この式を見てわかるとおり、濃度勾配が高ければ流束も速くなる。このとき、距離dを十分小さくしていくと次の式が成り立つ。(距離dを十分小さくしていき、距離⊿xにする)

 

　

 

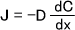
この式で表わされる関係をフィックの第一法則という。