役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 統計学 ＞ ピアソンの相関係数、Spearman(スピアマン)の順位相関係数

ピアソンの相関係数、Spearman(スピアマン)の順位相関係数

 

　回帰と相関
回帰とはxとyでどのような関係式で表すことができるかである。例えば、回帰直線はy=a＋bxの式で表され、aとbに何の数値が入るかを調べる。それに対し、相関はxとyの相互関係の強さである。

 

　

 

　ピアソンの相関係数(パラメトリック法)
相関の強さは相関係数rで表し、｜r｜≦1である。｜r｜が1に近いほど相関が強い。ただし、この検定はデータが正規分布するときに使用できる。

 

・仮説の設定
帰無仮説(H₀)：「相関はない」と仮定する。
対立仮説(H₁)：「相関はある」と仮定する。

 

・確率を求める
rを求めるのに必要な計算は回帰を求めるときと似ており、次の5つの式を計算する。

 

Σxi	………	xを全て足したもの
Σyi	………	yを全て足したもの
Σxi2	………	xの2乗を全て足したもの
Σyi2	………	yの2乗を全て足したもの
Σxiyi	………	xとyの積を全て足したもの

 

上記の計算をしたら、下の式によってS_xx,S_xy,S_yyを求める。

 

　

 

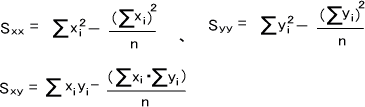
次に下の式によって統計量rを求める。

 

　

 

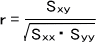
rを求めたら、相関係数検定表(r表)からr_αを求める。

 

・判定
｜r｜≦r_αのとき、P＞0.05となる → 帰無仮説を棄却できない。
｜r｜＞r_αのとき、P＜0.05となる → 帰無仮説を棄却する。

 

………………………………………………………………………………………………………………

 

　例題
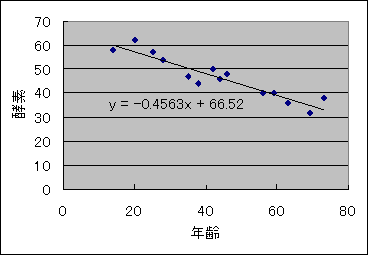
健康診断を行ったところ、年齢と酵素Xの値で下のような結果を得た。このとき、年齢と酵素Xの量には関連があるかどうかを検定せよ。ただし、「このデータは正規分布する」と仮定する。

 

年齢 酵素X 35 47 20 62 63 36 59 40 14 58 44 46 42 50

年齢 酵素X 25 57 73 38 38 44 56 40 69 32 28 54 46 48

 

(注：このデータは便宜的に作ったもので、実際のデータではない)

 

帰無仮説(H₀)：年齢と酵素Xの量には関連がない
対立仮説(H₁)：年齢と酵素Xの量には関連がある

 

・計算
まずΣx_i,Σy_i,Σx_i²,Σy_i²,Σx_iy_iを求めるためにx,y,x²,xy,y²の表を作る。

 

x	y	x2	xy	y2
35	47	1225	1645	2209
20	62	400	1240	3844
63	36	3969	2268	1296
59	40	3481	2360	1600
14	58	196	812	3364
44	46	1936	2024	2116
42	50	1764	2100	2500
25	57	625	1425	3249
73	38	5329	2774	1444
38	44	1444	1672	1936
56	40	3136	2240	1600
69	32	4761	2208	1024
28	54	784	1512	2916
46	48	2116	2208	2304
Σxi=612	Σyi=652	Σxi2=31166	Σxiyi=26488	Σyi2=31

 

Σx_i,Σy_i,Σx_i²,Σy_i²,Σx_iy_iを求めたら、今度は偏差平方和（S_xx,S_yy）と偏差積和（S_xy）を求める。

 

　

 

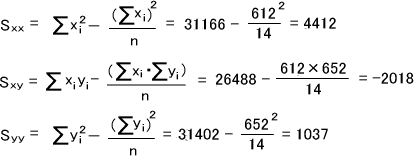
偏差平方和を求めたら、次は統計量rを求める。

 

　

 

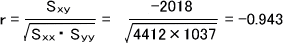
このときのr_0.05はn=14のとき相関係数検定表(r表)から、r_0.05=0.532であると分かる。

 

｜r｜=0.943＞0.532=r_0.05より、P＜0.05となるので帰無仮説を棄却できる。つまり、「年齢と酵素Xの量には関連がある」ということができる。

 

　

 

………………………………………………………………………………………………………………

 

　Spearmanの順位相関係数(ノンパラメトリック法)
データが正規分布するならピアソンの相関係数rで検定すればいいが、正規分布しないならSpearmanの順位相関係数r_sで検定する。

 

・仮説の設定
帰無仮説(H₀)：「相関はない」と仮定する。
対立仮説(H₁)：「相関はある」と仮定する。

 

・確率を求める
[計算法１]
まず、x,yごとに1→n番まで順位を付ける。順位を付けたら、対応するxの順位r_xiとyの順位r_yiの差d_iを求める。d_iを計算したら、その二乗d_i²を求める。

 

d_iとd_i²を求めることができたら、下の計算式によってr_sを導く。

 

　

 

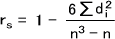
[計算法２]
xの順位r_xiとyの順位r_yiから相関係数を求める。(ピアソンの相関係数のときと同じ計算)

 

Σr_xi,Σr_yi,Σr_xi²,Σr_yi²,Σr_xir_yiを求めた後、偏差平方和（S_xx,S_yy）と偏差積和（S_xy）を計算して下の式に代入する。

 

　

 

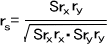
n≦30のとき、Spearman検定表から判定する。

 

・判定
P≧αのとき帰無仮説を棄却できない。
P＜αのとき帰無仮説を棄却する。

 

n＞30のとき、t=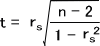が自由度df=n-2のt分布をする → ｔ分布表から判定

 

・判定
｜t｜≦t_αのとき、P≧αとなり帰無仮説を棄却できない。
｜t｜＞t_αのとき、P＜αとなり帰無仮説を棄却する。有意差あり。

 

………………………………………………………………………………………………………………

 

健康診断を行ったところ、年齢とある酵素の値で下のような結果を得た。このとき、年齢と酵素Xの量には関連があるかどうかを検定せよ。ただし、「このデータは正規分布しない」と仮定する。

 

年齢 酵素X 35 47 20 62 63 36 59 40 14 58 44 46 42 50

年齢 酵素X 25 57 73 38 38 44 56 40 69 32 28 54 46 48

(注：このデータは便宜的に作ったもので、実際のデータではない)

 

帰無仮説(H₀)：年齢と酵素Xの量には関連がない
対立仮説(H₁)：年齢と酵素Xの量には関連がある

 

・計算
[計算法１]
x,yについて順位をつけてr_xiとr_yiを導く。r_xiとr_yiの差d_iとその二乗d_i²を求める。

 

年齢	酵素X	順位		順位差
x	y	rxi	ryi	di	di2
35	47	5	8	-3	9
20	62	2	14	-12	144
63	36	12	2	10	100
59	40	11	4.5	6.5	42.25
14	58	1	13	-12	144
44	46	8	7	1	1
42	50	7	10	-3	9
25	57	3	12	-9	81
73	38	14	3	11	121
38	44	6	6	0	0
56	40	10	4.5	5.5	30.25
69	32	13	1	12	144
28	54	4	11	-7	49
46	48	9	9	0	0

 

　Σd_i²=874.5

 

d_i²の和(Σd_i²)の値は874.5なので、下の式に代入してr_sを求める。

 

　

 

[計算法２]
Σr_xi,Σr_yi,Σr_xi²,Σr_yi²,Σr_xir_yiを求めた後、偏差平方和（S_xx,S_yy）と偏差積和（S_xy）を計算する。

 

rxi	ryi	rxi2	rxiryi	ryi2
5	8	25	40	64
2	14	4	28	196
12	2	144	24	4
11	4.5	121	49.5	20.25
1	13	1	13	169
8	7	64	56	49
7	10	49	70	100
3	12	9	36	144
14	3	196	42	9
6	6	36	36	36
10	4.5	100	45	20.25
13	1	169	13	1
4	11	16	44	121
9	9	81	81	81
Σxi=105	Σyi=105	Σxi2=1015	Σxiyi=577.5	Σyi2=1014.5

 

・Sr_xr_x = 227.5
・Sr_xr_y = -210
・Sr_yr_y = 227

 

次に、下の式に代入してr_sを求める。

 

　

 

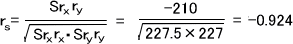
n≦30なので、Spearman検定表から判定する。n=8のとき、P＜0.05となる最小のr_s値は0.539である。つまり、r_sが0.539よりも値が大きければ帰無仮説を棄却できる。

 

ここでは｜r｜＞0.539なので、P＜0.05となり帰無仮説を棄却できる。つまり、「年齢と酵素Xの量には関連がある」と判断できる。