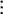役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 統計学 ＞ 二元配置分散分析法、Friedman(フリードマン)検定 (関連多群)

二元配置分散分析法、Friedman(フリードマン)検定 (関連多群)

 

　独立多群と関連多群
独立多群は一つの要因によって分類されるが、関連多群は二つの要因によって分類される。関連多群で一番典型的な例は時間による変化である。下に「薬物の濃度」と「生菌数」の推移の表を示す。

 

	0（h）	1（h）	2（h）	3（h）	…
濃度a（%）	100	90	80	73	…
濃度b（%）	100	80	70	60	…
濃度c（%）	100	60	45	34	…

 

　

 

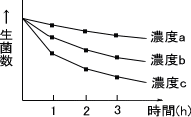
ただし、薬剤の濃度が濃すぎると急激に菌を殺してしまうため、下の図のように変化してしまう。

 

　

 

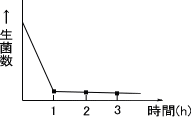
この図では0→1の一つのポイントでは変化があるが、1→2→3でほとんど変化がない。このような作用を相互作用といい、実際の検定をする場合は相互作用を考慮しなければならない。

 

しかし、相互作用を考慮すると計算がかなり面倒になるのでここでは省略する。

 

　二元配置分散分析法(パラメトリック法)
関連多群で二元配置分散分析法をするかFriedman検定をするかは、Bartlett検定で「各群の分散が等しい」と判断されるかどうかで決定する。

 

「各群の分散が等しい」ならば二元配置分散分析法で検定し、「各群の分散が等しくない」ならばFriedman検定で検定する。ただし、関連多群の場合は行・列で二回のBartlett検定が必要。

 

・仮説の設定
帰無仮説(H₀)：「各群で差がない」と仮定する。
対立仮説(H₁)：「各群で差がある」と仮定する。

 

・確率を求める
統計量を求めるには、平均値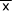,総平均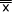を求める必要がある。

 

	B1	B2		Bc	平均値
A1	○	○	…	○	1
A2	○	○	…	○	2
Ar	○	○	…	○	r
平均値	1	2		c

 

　総平均＝…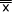

 

平均値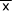,総平均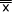を求めたら、これらの値を使って行間変動S_A、列間変動S_B、総変動S_Tを計算する。下にそれぞれの式を示す。(c=列の群数、r=行の群数)

 

・行間変動

 

偏差平方和S_A

 

　

 

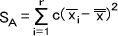
自由度df_A=r-1

 

・列間変動

 

偏差平方和S_B

 

　

 

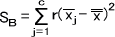
自由度df_B=c-1

 

・総変動

 

偏差平方和S_T

 

　

 

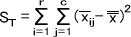
自由度df_T=r・c-1

 

行間変動、列間変動、総変動の偏差平方和と自由度を求めると、そこから誤差変動を計算する。その後、分散値を計算して分散比Fを求める。

 

	偏差平方和	自由度	分散	分散比F
行間変動	SA	dfA=r-1	sA2=SA/dfA	FA=sA2/sE2
列間変動	SB	dfB=c-1	sB2=SB/dfB	FB=sB2/sE2
誤差変動	SE=ST-SA-SB	dfE=dfT-dfA- dfB	sE2=SE/dfE	－
総変動	ST	dfT=r・c-1

 

行間の差の検定の場合、自由度df_A(=df₁), df_E(=df₂)でF分布表からF_αを求めて計算したF値と比べる。また、列間の差の検定の場合は自由度df_B(=df₁), df_E(=df₂)のF分布に従う。

 

・判定
1≦F≦F_αのとき、P＞0.05となる→帰無仮説を棄却できない。
F＞F_αのとき、P＜0.05となる→帰無仮説を棄却する。

 

………………………………………………………………………………………………………………

　例題
A,B,C高校で進学を希望する大学の調査を行った。そのときD,E,F,G大学にはそれぞれ次の数の生徒が希望した。このとき、大学によって人気の違いがあるといえるか。また、高校によって希望する大学に偏りがあるか検定せよ。

 

	D大学	E大学	F大学	G大学	平均値	分散
A高校	8	5	7	10	7.5	3.3
B高校	3	1	3	7	3.5	4.8
C高校	6	3	2	5	4	2.5
平均値	5.7	3	4	7.3
分散	4.2	2.7	4.7	4.2

 

　r=3,c=4,総平均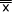＝5
(注：このデータは便宜的に作ったもので、実際のデータではない)

 

・行に注目
帰無仮説(H₀)：高校によって希望する大学に偏りがない。
対立仮説(H₁)：高校によって希望する大学に偏りがある。

 

・列に注目
帰無仮説(H₀)：大学の希望に差がない。
対立仮説(H₁)：大学の人気に差がある。

 

・Bartlett検定
帰無仮説(H₀)：各群の分散は均一である
対立仮説(H₁)：各群の分散は均一でない

 

・行に注目
M,Cを計算するとM=0.321,C=1.15でX²=0.28である。自由度df=3-1=2のX²分布表より、X²_0.05=5.991となる。

 

X²＜X²_0.05なので、P＞0.05となり帰無仮説を棄却できない → 「各群の分散に差がある」とはいえない

 

・列に注目
M,Cを計算するとM=0.168,C=1.15でX²=0.15である。自由度df=4-1=3のX²分布表より、X²_0.05=7.815となる。

 

X²＜X²_0.05なので、P＞0.05となり帰無仮説を棄却できない → 「各群の分散に差がある」とはいえない

 

行・列の分散が均一なので二元配置分散分析法を行う。

 

・二元配置分散分析法
○行間変動を求める

 

　
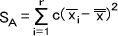
　　　=4(7.5-5)² ＋4(3.5-5)² ＋4(4-5)²
　　　=38

 

自由度df_A=r-1=3-1=2

 

○列間変動を求める

 

　
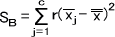
　　　=3(5.7-5)² ＋3(3-5)² ＋3(4-5)² ＋3(7.3-5)²
　　　=32.3

 

自由度df_B=c-1=4-1=3

 

○総変動を求める

 

　
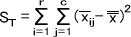
　　　={(8-5)² ＋(5-5)² ＋(7-5)² ＋(10-5)² }
　　　　{(3-5)²＋ (1-5)² ＋(3-5)² ＋(7-5)² }
　　　　{(6-5)² ＋(3-5)²＋ (2-5)² ＋(5-5)² }
　　　=38＋28＋14=80

 

自由度df_T=r×c-1=3×4-1=12-1=11

 

行間変動、列間変動、総変動から誤差変動を求めて分散分析表にまとめると下のようになる。

 

	偏差平方和	自由度	分散	分散比F
行間変動	SA	dfA=r-1	sA2=SA/dfA	FA=sA2/sE2
	38	2	19	11.9
列間変動	SB	dfB=c-1	sB2=SB/dfB	FB=sB2/sE2
	32.3	3	10.8	6.75
誤差変動	SE=ST-SA-SB	dfE=dfT-dfA- dfB	sE2=SE/dfE	－
	9.7	6	1.6	－
総変動	ST	dfT=r・c-1
	80	11

 

・行に注目
F分布表より、df_A=2, df_E=6のときF_0.05=19.33

 

F=11.9＞5.14=F_0.05より、P＜0.05となり帰無仮説を棄却できる。よって、「高校によって希望する大学に偏りがある」ということができる。

 

・列に注目
F分布表より、df_A=3, df_E=6のときF_0.05=8.94

 

F=6.75＞4.76=F_0.05より、P＜0.05となり帰無仮説を棄却できる。よって、「大学の人気に差がある」ということができる。

 

………………………………………………………………………………………………………………

 

　Friedman検定(ノンパラメトリック法)
Bartlett検定で「各群の分散が等しくない」と判定されたら二元配置分散分析法ではなく、Friedman検定を用いる。Friedman検定では順位の付け方が2通りある。

 

・仮説の設定
帰無仮説(H₀)：「各群で差がない」と仮定する。
対立仮説(H₁)：「各群で差がある」と仮定する。

 

・確率を求める
○行(要因B)を検定する場合
列(要因A)の各群ごとに順位をつける。その後、順位を足してR_iを求める。
(行数をk,列数をnとする)

 

○列(要因A)を検定する場合
行(要因B)の各群ごとに順位をつける。その後、順位を足してR_iを求める。
(行数をn,列数をkとする)

 

　　　

 

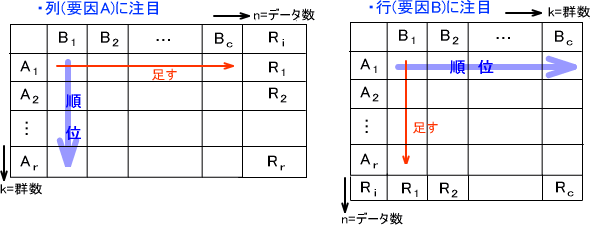
R_iを求めたら、下の式によって統計量X²rを求める。

 

　

 

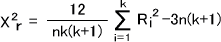
確率を求めるとき、群数kによって求め方が異なる。下にそれぞれの確率の求め方を示す。

 

・k≦4のとき → Friedman検定表から求める
・判定
P≧αのとき帰無仮説を棄却できない。
P＜αのとき帰無仮説を棄却する。

 

・k＞4のとき → X²rは近似的に自由度df=k-1のX²分布に従う → X²分布表
・判定
X²≦X²_αのとき、P≧αとなり帰無仮説を棄却できない
X²＞X²_αのとき、P＜αとなり帰無仮説を棄却する

 

………………………………………………………………………………………………………………

 

　例題
マウスに薬剤Xを投与し、血糖値を観察した。投与前後で血糖値が変化したといえるかどうか検定せよ。ただし、「各時間での分散は均一でない」とする。

 

	投与前	投与直前	1時間後	2時間後	3時間後
a	162	60	88	143	160
b	160	50	112	136	156
c	150	100	135	149	152
d	155	92	85	115	148

 

(注：このデータは便宜的に作ったもので、実際のデータではない)

 

帰無仮説(H₀)：投与前後で血糖値に変化がない。
対立仮説(H₁)：投与前後で血糖値に変化がある。

 

・計算

 

投与前後での血糖値の変化を見るので行(時間)に注目する。まず、列(マウス)ごとに数値の小さい順に順位をつける。そして、順位を群ごとに足してR_iを求める。

 

	投与前	投与直前	1時間後	2時間後	3時間後
a	5	1	2	3	4
b	5	1	2	3	4
c	4	1	2	3	5
d	5	2	1	3	4
Ri	19	5	7	12	17

 

(行に注目するので、n=4,k=5となる)

 

R_iを求めたら、下の式によって統計量X²rを求める。

 

　

 

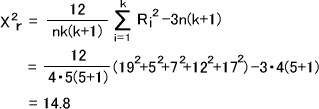
k＞4なので、計算したX²r値は近似的に自由度df=k-1=5-1=4のX²分布に従う。X²分布表より、X²_0.05=9.488である。

 

X²r=14.8＞9.488=X²_0.05なので、P＜0.05となり帰無仮説を棄却できる。つまり、「投与前後で血糖値に変化がある」ということができる。