Mann-Whitney (マン・ホイットニイ)検定
Mann-Whitney検定(ノンパラメトリック法)
Mann-Whitney検定は独立2群の差を検定するときのノンパラメトリックな方法である。
・統計量Uの求め方
Mann-Whitney検定では統計量としてUを求めなければならない。統計量Uの求め方であるが、片方の群のそれぞれの点に注目して、個々の点よりも大きい他方のデータ数を数える。
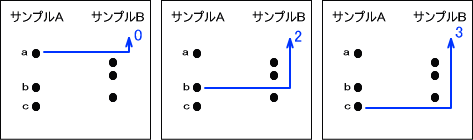
上の図でサンプルAに注目すると、aより大きい値はサンプルBにはない。bより大きい値はサンプルBに2つ、cより大きい値はサンプルBに3つある。この場合、統計量Uは+3=5となる。
ただし、サンプルBに注目して個々の点よりも大きい他方のデータ数を数えてもよい。この場合の統計量Uは1+1+2=4となる。統計量Uを求めるとき、どちらに注目してもよい。(普通、注目するのは数えやすい方にする)
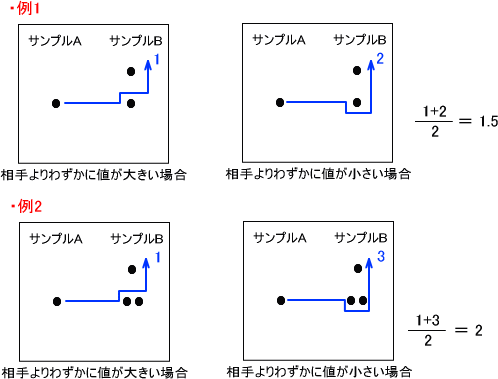
もし、両群に同じ値があるなら「相手よりわずかに値が大きい場合」と「相手よりわずかに値が小さい場合」を想定してその平均値をとる。
・仮説の設定
帰無仮説(H0):「2群間に差がない」と仮定する。
対立仮説(H1):「2群間に差がある」と仮定する。
・確率を求める
まず、統計量Uを求める。
n1≦20かつn2≦20のとき、Mann-Whitney検定表よりU値がそれ以上極端となる確率Pを求める。
・判定
P≧αのとき帰無仮説を棄却できない。
P<αのとき帰無仮説を棄却する。有意差あり。
・確率を求める
それに対しn1またはn2の一方が20より大きいとき、下の式から平均値と標準偏差を出してz値を出す。この式によってUの分布は近似的に正規分布する。
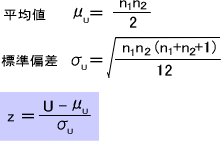
その後、標準正規分布表から確率Pを求める。
………………………………………………………………………………………………………………
例題(小標本)
大腸がんを患っている患者と胃がんを患っている患者に鎮痛薬Xを投与した。このとき、薬がどれくらい効き目があったかを医師にアンケートをとって、20段階で評価してもらった。大腸がんと胃がんで鎮痛薬Xに効果の違いがあるといってよいか検定しなさい。
大腸がん |
20 |
18 |
15 |
13 |
10 |
6 |
|
|
胃がん |
17 |
16 |
12 |
9 |
8 |
6 |
4 |
2 |
(注:このデータは便宜的に作ったもので、実際のデータではない)
帰無仮説:大腸がんと胃がんで鎮痛薬Xに効果の違いはない
対立仮説:大腸がんと胃がんで鎮痛薬Xに効果の違いがある
・計算
統計量Uを求める。この場合では大腸がんの群に注目してU値を求める。U値は次のようになる。
U値 = 2+2+3 +.5 = 12.5
n1≦20かつn2≦20なので、Mann-Whitney検定表よりU値がそれ以上極端となる確率Pを求める。n1=6、n2=8のときの両側確率P<0.05となるU値の下側有意点は8である。
計算したU値は8よりも大きいので、P≧0.05となり帰無仮説を棄却できない。よって、「大腸がんと胃がんで鎮痛薬Xに効果の違いがある」とはいえない。
………………………………………………………………………………………………………………
例題(大標本)
A大学の野球部とサッカー部に10種類の体力テストを実施し、それぞれ5段階で評価した。このときのスコアを個人別に求めるとしたのようになった。このとき、野球部とサッカー部で体力テストのスコアに差があるといってよいか検定しなさい。
|
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
(注:このデータは便宜的に作ったもので、実際のデータではない)
帰無仮説:野球部とサッカー部で体力テストのスコアに差はない
対立仮説:野球部とサッカー部で体力テストのスコアに差がある
・計算
統計量Uを求めるのだが、この場合では野球部に注目してU値を求める。このときの計算は次のようになる。
U値 = 2+3+3+4+4+4+8+9+9+9.5+10+10.5+11+11+12+12+13 = 135
次の式によって平均値と標準偏差を求め、その後z値を求める。この式でUは近似的に正規分布となる。
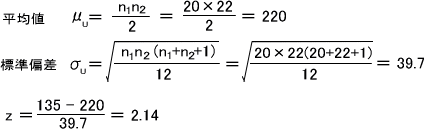
計算したZ値より、標準正規分布表から確率Pを求めるとP = 0.03236<0.05 となる。P<0.05なので帰無仮説を棄却し対立仮説を採用する。つまり、「野球部とサッカー部で体力テストのスコアに差がある」ということができる。
スポンサードリンク
カテゴリー
スポンサードリンク
