役に立つ薬の情報〜専門薬学＞統計学＞Kendall(ケンドール)の一致係数
役に立つ薬の情報〜専門薬学 サイトマップ


　　　Kendall(ケンドール)の一致係数
　Kendallの一致係数W(ノンパラメトリック法)
Kendallでは関連多群での相関を判定することができる。なお、これはノンパラメトリック法である。

・仮説の設定
帰無仮説(H0)：「相関はない」と仮定する。
対立仮説(H1)：「相関はある」と仮定する。

・確率を求める
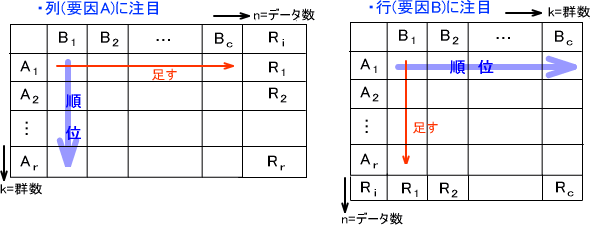
○行(要因B)を検定する場合
列(要因A)の各群ごとに順位をつける。その後、順位を足してRiを求める。
(行数をk,列数をnとする)

○列(要因A)を検定する場合
行(要因B)の各群ごとに順位をつける。その後、順位を足してRiを求める。
(行数をn,列数をkとする)

※ここまでの手順はFriedman検定のときと同じである

　　　

Riを求めたら、Riの偏差平方和Sを次の式によって求める。

　

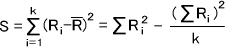
※別に求めなくてもよいが、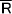を使って偏差平方和Sを求める場合は下の式を使って導き出す。

　

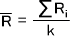
偏差平方和Sを求めたら次の公式によってWを求める。なお、Wの取りうる値は0≦W≦1である。

　

次は、下の式によってX2rを求める。

　

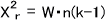
Friedman検定のときと同じように判定する。

・k≦4のとき → Friedman検定表から求める
・判定
P≧αのとき帰無仮説を棄却できない。
P＜αのとき帰無仮説を棄却する。

・k＞4のとき → X2rは近似的に自由度df=k-1のX2分布に従う → X2分布表
・判定
X2≦X2αのとき、P≧αとなり帰無仮説を棄却できない
X2＞X2αのとき、P＜αとなり帰無仮説を棄却する

………………………………………………………………………………………………………………

　例題
理系の学生6人に好きな科目のアンケートをとった。学生が好きな科目に一貫性があるかどうかを判定せよ。

　 国語 数学 英語 物理 化学 地理・歴史
A 6 2 4 1 3 5
B 5 1 4 2 3 6
C 5 2 5 3 1 4
D 6 5 2 3 1 4
E 5 3 4 1 2 6
F 5 1 6 2 3 4
(注：このデータは便宜的に作ったもので、実際のデータではない)

帰無仮説(H0)：学生が好きな科目に一貫性がない
対立仮説(H1)：学生が好きな科目に一貫性がある

・計算
好きな科目に一貫性があるかどうかを判定するので、行(科目)に注目する。最初から順序尺度のデータなので、そのまま各群で順位を足してRiを求める。

　 国語 数学 英語 物理 化学 地理・歴史 　
A 6 2 4 1 3 5
B 5 1 4 2 3 6
C 5 2 5 3 1 4
D 6 5 2 3 1 4
E 5 3 4 1 2 6
F 5 1 6 2 3 4
G 4 2 5 3 1 4
Ri 36 16 30 15 14 33 ΣRi=144
Ri2 1296 256 900 225 196 1089 ΣRi2=3962
　(ΣRi)2 = 1442 = 20736 、 n=7,k=6

これらの数値から、下の式によってRiの偏差平方和Sを求める。

　

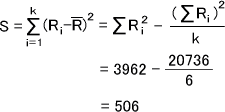
次に、Sから下の式によってWを求める。

　

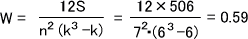
Wを求めたら、次の式によってX2rを求める。

　

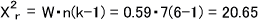
k＞4なので、X2rは近似的に自由度df=k-1=6-1=5のX2分布に従う。X2分布表より、X20.05=11.071である。

X2=20.65＞11.071=X20.05なので、P＜0.05となり帰無仮説を棄却できる。よって、「学生が好きな科目に一貫性がある」ということができる。