役に立つ薬の情報〜専門薬学＞統計学＞直線回帰
役に立つ薬の情報〜専門薬学 サイトマップ


　　　直線回帰
　回帰と相関
回帰とはxとyでどのような関係式で表すことができるかである。例えば、回帰直線はy=a+bxの式で表され、aとbに何の数値が入るかを調べる。それに対し、相関はxとyの相互関係の強さである。

　　　

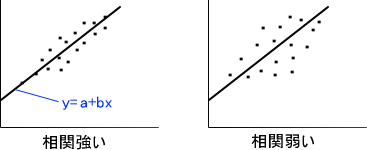
相関の強さは相関係数rで表し、｜r｜≦1である。｜r｜が1に近いほど相関が強い。

　直線回帰(最小二乗法)
平面に当てはめたn個の点からy=a+bxの式を導き出すのが直線回帰である。この直線を回帰直線という。

係数a,bを導くためには横軸をx,縦軸をyとしたとき、次の5つの式を計算しないといけない。

・Σxi ……… 　xを全て足したもの
・Σyi ……… 　yを全て足したもの
・Σxi2 ……… 　xの2乗を全て足したもの
・Σyi2 ……… 　yの2乗を全て足したもの
・Σxiyi　 ……… 　xとyの積を全て足したもの

上記の計算をしたら、下の式に代入してa,bを求める。

　

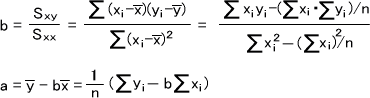
ここでSxxはxの偏差平方和、Sxyはx,yの偏差平方和を表している。下に、Sxx,Sxy,Syyの求め方を示す。(Syyはyの偏差平方和)

　

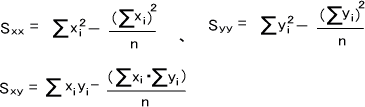
・回帰の優位性を判断する
回帰直線を求めても、その回帰が有意(意味のあるもの)でなければならない。回帰の優位性を求めるには、傾きであるbが0から偏っているかどうかを検定する。bの信頼区間係数βに0が含まれていればその回帰は意味のないものであり、0が含まれていなければその回帰は意味のあるものである。

bの優位性を判定するには、まずbの標準偏差sbを求める必要がある。sbは下の式によって求めることができる。

　

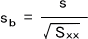
ここで、sは回帰直線の標準偏差であり、下の式で求める。

　

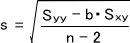
Sbを求めたら今度はt0.05をt分布表から求める。このときの自由度dfはn-2である。

Sbとt0.05を求めたらbの信頼区間係数βを求める。95％の信頼区間係数βは次の式によって求めることができる。

　

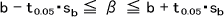
・判定
信頼区間係数βに0が含まれる → 回帰は有意でない
信頼区間係数βに0が含まれない → 回帰は有意である

………………………………………………………………………………………………………………

　例題
体重と身長の関係を調べると、表のような結果を得られた。
(1)最小二乗法によって回帰直線y=a+bxを求めよ。
(2)bの信頼区間を求めよ。
(3)回帰は有意かどうかを判断せよ。

体重 身長
65 170
80 182
72 174
57 162
78 172
67 166
58 158
体重 身長
92 182
68 177
65 175
58 164
70 169
62 177
84 182
(注：このデータは便宜的に作ったもので、実際のデータではない)

・問１
まずΣxi,Σyi,Σxi2,Σyi2,Σxiyiを求めるためにx,y,x2,xy,y2の表を作る。

x y x2 xy y2
65 170 4225 11050 28900
80 182 6400 14560 33124
72 174 5184 12528 30276
57 162 3249 9234 26244
78 172 6084 13416 29584
67 166 4489 11122 27556
58 158 3364 9164 24964
92 182 8464 16744 33124
68 177 4624 12036 31329
65 175 4225 11375 30625
58 164 3364 9512 26896
70 169 4900 11830 28561
62 177 3844 10974 31329
84 182 7056 15288 33124
Σxi=976 Σyi=2410 Σxi2=69476 Σxiyi=168833 Σyi2=415636


Σxi,Σyi,Σxi2,Σyi2,Σxiyiを求めたら、今度は偏差平方和(Sxx,Sxy,Syy)を求める。 (Syyは回帰の優位性を判断するときに使う)

　

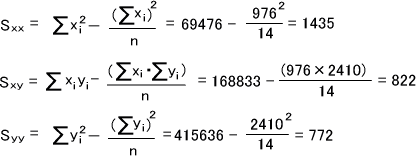
偏差平方和を求めたら、次は係数a,bを求める。

　

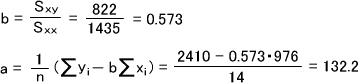
よって、回帰直線は次のようになる。(下の式では)

　y = 132.2 + 0.573x

　　　

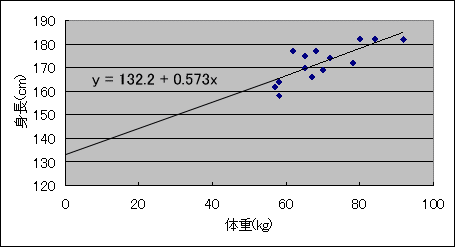
※直線に限らず、エクセルを使えば回帰を簡単に計算してくれます。

・問２
回帰の優位性を判断するため、回帰直線の標準偏差sを求める。

　

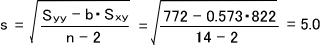
次にbの標準偏差sbを求める。

　

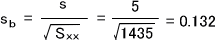
また、t0.05は自由度df=n-2=14-2=12のt分布表よりt0.05=2.179となる。信頼区間係数βはsbとt0.05を使って次の式で求める。

　

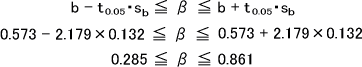
・問３
bの信頼区間の中にb=0を含まないので、「回帰は有意である」と判断することができる。