一元配置分散分析法、Kruskal-Wallis(クラスカル・ワリス)検定 (独立多群)
多群の検定
群数が二つなら二標本の検定をするが、三つ以上の群がある場合は多群での検定をする必要がある。独立多群の検定では「データのどこかに差があるかどうか」を検定する。ただし、どことどの群で差があるかまでは分からない。
多群を検定するとき、「それぞれの群を二標本t検定で検定すればよいのでは」と疑問が生じてくるが、実際にこの方法を行ってはいけない。これは、判定を間違ってしまう確率が高くなるからである。
二群の検定で判定が有意差「無」と判断される確率は(1-α)である。それでは、二群の検定を三回行った場合で三つとも有意差「無」と判断される確率は(1-α)3となる。このとき、逆に有意差「有」と判断される確率は1-(1-α)3となってしまう。
もし、検定をn回するなら(間違って)有意差「有」と判断される確率は1-(1-α)nとなってしまう。(5群で有意差を検定すると約40％、10群では90％の確率で有意差「有」と判断される)
つまり、二標本t検定で多群を検定すると高い確率で有意差「有」と判断され、実際には「差がない」のに「差がある」と誤って判断してしまう。これでは検定をしても意味がない。これを回避するため、多群を同時に比較する検定をする必要がある。
一元配置分散分析法(パラメトリック法)
この検定は独立多群の検定であり、「各群の分散が等しい」という条件がある。各群の分散が等しいかどうかはBartlett検定を用いる。もしBartlett検定で各群の分散が等しくないと判断されたらKruskal-Wallis検定を使う。
・仮説の設定
帰無仮説(H0)：「各群で差がない」と仮定する。
対立仮説(H1)：「各群で差がある」と仮定する。
・確率を求める
統計量を求めるには、まずデータ数n,平均値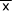
,分散s2,総平均
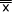を求める必要がある。
|
測定値 |
データ数 |
平均値 |
分散 |
A1 |
○○…○ |
n1 |
|
s12 |
A2 |
○○…○ |
n2 |
|
s22 |
|
|
|
|
|
Ak |
○○…○ |
nk |
|
sk2 |
総平均＝…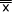
データ数n,平均値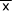,分散s2,総平均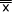を求めたら、これらの値を使って群間変動と群内変動を計算する。下にそれぞれの式を示す。
・群間変動
偏差平方和SA
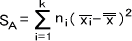
自由度dfA=k-1
・群内変動
偏差平方和SE
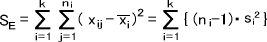
自由度dfE=N-k (N=n1＋n2＋… nk)
群間変動と群内変動の偏差平方和と自由度を求めると、そこから分散値を計算して分散比Fを求める。
|
偏差平方和 |
自由度 |
分散 |
分散比F |
群間変動 |
SA |
dfA=k-1 |
sA2=SA/dfA |
 |
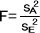群内変動 |
SE |
dfE=N-k |
sE2=SE/dfE |
自由度dfA(=df1), dfE(=df2)でF分布表からFαを求めて計算したF値と比べる。
・判定
1≦F≦Fαのとき、P＞0.05となる→帰無仮説を棄却できない。
F＞Fαのとき、P＜0.05となる→帰無仮説を棄却する。
………………………………………………………………………………………………………………
例題
あるホルモンの活性を調べると、次のような結果を得た。群間に差があるかどうかを検定せよ。
|
データ数 |
平均値 |
分散 |
||||
A群 |
21 |
23 |
19 |
25 |
4 |
22 |
5 |
B群 |
10 |
6 |
14 |
|
3 |
10 |
10.7 |
C群 |
25 |
31 |
29 |
23 |
4 |
27 |
10 |
D群 |
14 |
16 |
21 |
|
3 |
17 |
8.7 |
総平均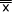＝19.79
(注：このデータは便宜的に作ったもので、実際のデータではない)
総平均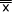は平均値を足して割った値 {(22＋10＋27＋17)/4=19} ではない。すべてのセルの値を足して、その数で割った値である。
帰無仮説(H0)：ホルモン活性に差がない。
対立仮説(H1)：ホルモン活性に差がある。
・計算
一元配置分散分析法をするかKruskal-Wallis検定をするかは、Bartlett検定によって「各群の分散が等しいかどうか」を決定して判断する。
・Bartlett検定
帰無仮説(H0)：各群の分散は均一である
対立仮説(H1)：各群の分散は均一でない
まず、群内変動を計算する。各群の分散からsEを求めると、次のようになる。
sE =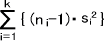 
= 3×5＋2×10.7＋3×10＋2×8.7 = 83.7
sE2 = 83.7/(N-k) = 83.7/10 = 8.37
M値とC値を計算して、X2値を求めるとX2=0.833となる。自由度df=k-1=4-1=3のX2分布表より、X20.05=7.815となる。
X2＜X20.05なので、P＞0.05となり帰無仮説を棄却でない。
(各群の分散は均一と判断 → 一元配置分散分析法を行う)
・一元配置分散分析法
群内変動はBartlett検定をするときにすでに計算しているので求めなくてよい。ここでは、群間変動を計算する。
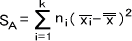
= 4×(22-19.57)2 ＋3×(10-19.57)2 ＋4×(27-19.57)2 ＋3×(17-19.57)2
= 539
群間変動と群内変動を分散分析表にまとめると、下のようになる。
|
偏差平方和 |
自由度 |
分散 |
分散比F |
|
群間変動 |
SA |
dfA=k-1 |
sA2=SA/dfA |
|
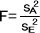F=15.3 |
|
539 |
3 |
180 |
||
群内変動 |
SE |
dfE=N-k |
sE2=SE/dfE |
||
|
117.9 |
10 |
11.79 |
||
F分布表より、dfA=3, dfE=10のときF0.05=3.71
F=15.3＞3.71=F0.05より、P＜0.05となり帰無仮説を棄却できる。よって、「ホルモン活性に差がある」ということができる。
………………………………………………………………………………………………………………
Kruskal-Wallis検定(ノンパラメトリック法)
Bartlett検定で「各群の分散は均一である」と判断されれば一元配置分散分析法をすればよいが、「各群の分散は均一でない」と判断されたならKruskal-Wallis検定をする。
・仮説の設定
帰無仮説(H0)：「各群で差がない」と仮定する。
対立仮説(H1)：「各群で差がある」と仮定する。
・確率を求める
Kruskal-Wallis検定では、まずすべてのデータを小さいものから1番→2番→……→N番と順位を付ける。この順位を各群ごとに足してRiを求める。Riを求めたら、下の計算式によって統計量Hを計算する。(N=データの総数、k=群数)
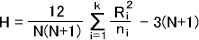
確率を求めるとき、条件によって異なる求め方をしないといけない。下にそれぞれの確率の求め方を示す。
・k=3かつN≦17のとき → Kruskal-Wallis検定表から求める
・判定
P≧αのとき帰無仮説を棄却できない。
P＜αのとき帰無仮説を棄却する。
・上の条件以外のとき → Hは近似的に自由度df=k-1のX2分布に従う → X2分布表
・判定
X2≦X2αのとき、P≧αとなり帰無仮説を棄却できない
X2＞X2αのとき、P＜αとなり帰無仮説を棄却する
………………………………………………………………………………………………………………
例題
あるホルモンの活性を調べると、次のような結果を得た。群間に差があるかどうかを検定せよ。
|
データ数 |
平均値 |
分散 |
||||
A群 |
21 |
23 |
19 |
25 |
4 |
22 |
5 |
B群 |
10 |
6 |
14 |
|
3 |
10 |
10.7 |
C群 |
25 |
31 |
29 |
23 |
4 |
27 |
10 |
D群 |
14 |
16 |
21 |
|
3 |
17 |
8.7 |
(注：このデータは便宜的に作ったもので、実際のデータではない)
このデータは一元配置分散分析法のときと全く同じ問題である。このデータはBartlett検定で「各群の分散は均一である」と判断されているが、ここでは「各群の分散は均一でない」として検定を進める。
帰無仮説(H0)：ホルモン活性に差がない。
対立仮説(H1)：ホルモン活性に差がある。
・計算
まず、データを小さい順で1から14番まで順位をつける。そのときの順位は下のようになる。
|
Ri |
||||
A群 |
7.5 |
9.5 |
6 |
11.5 |
34.5 |
B群 |
2 |
1 |
3.5 |
6.5 |
|
C群 |
11.5 |
14 |
13 |
9.5 |
48 |
D群 |
3.5 |
5 |
7.5 |
16 |
|
N = 4＋3＋4＋3 = 14
順位を足してRiを求めたら、次の式によって統計量Hを計算する。
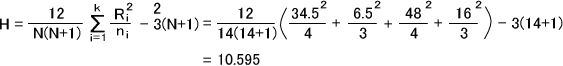
この場合、k=3かつN≦17ではないのでX2αを求める。X2分布表よりX20.05=7.815であると分かる。このときの自由度はdf=k-1=4-1=3である。
X2 = 10.595 ＞ 7.815 = X20.05 より、P＜0.05となり帰無仮説は棄却される。よって、「ホルモン活性に差がある」といえます。
スポンサードリンク
カテゴリー
スポンサードリンク