役に立つ薬の情報〜専門薬学＞統計学＞符号検定
役に立つ薬の情報〜専門薬学 サイトマップ


　　　符号検定
　符号検定(ノンパラメトリック法)
符号検定では各ペアの差の符号(+or-)に注目して検定する。この+と-の数には有意に差があるといってよいかを調べる検定である。

・仮説の設定
帰無仮説(H0)：「2群間に差がない」と仮定する。
対立仮説(H1)：「2群間に差がある」と仮定する。

・確率を求める
2群間に差がないならば、+と-の符号がでる確率は両方とも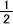である。もし、2群間に差があるならば+と-の符号がでる確率はどちらかに偏るはずである。

符号検定では+と-の符号を見るので、各ペアの差が0のペアはデータから除外する。また、符号の数が少ない方の個数をrとする。

帰無仮説が成立するならrが出現する確率は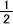であり、二項分布に従うことになる。この計算によってr値がその値以上の極端な値をとる確率を求める。

データの数nが5＜n≦25ならば直接計算して確率を求めればよい。ただし、n＞25であるなら下の式より平均値と標準偏差を出して、その後z値をだす。

　

z値を求めたら標準正規分布表から確率Pを求める。

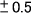であるがr＜n/2のときはr+0.5を、r＞n/2のときはr-0.5とする。これは正規分布の近似をよりよくするためである。

・判定
P≧αのとき、帰無仮説を棄却できない。
P＜αのとき、帰無仮説を棄却する。有意差あり。

………………………………………………………………………………………………………………

　例題(小標本)
料理Aと料理Bのどちらがおいしいかを13人が5段階で評価したとする。このとき、料理Aと料理Bのおいしさに差があるといってよいか。

料理A 料理B 符号
5 3 +
3 5 -
4 3 +
4 3 +
3 5 -
4 2 +
4 2 +
1 1 0
3 4 -
3 2 +
5 2 +
3 3 0
(注：このデータは便宜的に作ったもので、実際のデータではない)

帰無仮説：料理Aと料理Bのおいしさに差がない。
対立仮説：料理Aと料理Bのおいしさに差がある。

・計算
+の数を数えると7、-の数は3、差が0の数は2である。符号の数が少ない方の個数をrとするので、r値は3となる。また、データ数nは差が0のデータを除外するのでn＝12-2＝10 となる。

r値がその値以上の極端な値をとる確率を求めればいいので、この場合はr値以下がでる確率(r＝3,2,1,0となる確率)を求める。この場合であれば、「ある一方の料理の方が美味しい」or「ある一方の料理の方が不味い」と言うときの確率を求める。

なお、帰無仮説が成立していると仮定しているので出現率は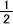である。

　

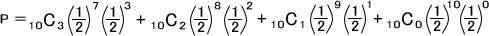
　　＝0.171875

※片側検定なら計算したP値と0.05を比較すればよいが、両側検定なら計算したP値×2と0.05を比較する。

この場合は両側検定なのでP×2 ＝ 0.34375 ＞ 0.05となり帰無仮説を棄却できない。つまり、「料理Aと料理Bのおいしさに差がある」とは言えない。

なお、ほとんど場合は両側検定である。片側検定となるのは、ある一方に行くと死んでしまうなどの片側にしかずれないことが明白なときである。

………………………………………………………………………………………………………………

　例題(大標本)
テレビ番組で料理Aと料理Bのどちらがおいしいかを30人が5段階で評価したとする。このとき、料理Aと料理Bのおいしさに差があるといってよいか。

料理A 料理B 符号
5 3 +
3 5 -
4 3 +
4 3 +
3 5 -
4 2 +
4 2 +
1 1 0
3 4 -
2 2 +
5 2 +
3 3 0
2 4 -
3 3 0
5 2 +
4 3 +
2 5 -
3 2 +
5 3 +
4 3 +
1 3 -
2 2 0
3 2 +
2 4 -
3 1 +
5 4 +
2 4 -
3 5 -
3 4 -
5 4 +
(注：このデータは便宜的に作ったもので、実際のデータではない)

帰無仮説：料理Aと料理Bのおいしさに差がない。
対立仮説：料理Aと料理Bのおいしさに差がある。

・計算
+の数は16、-の数は10、差が0の数は4である。符号の数が少ない方の個数をrとするので、r値は10となる。また、データ数nは差が0のデータを除外するのでn＝30-4＝26 となる。

平均値はn/2 ＝ 26/2 ＝ 13 となり、標準偏差は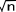/2 ＝ 5.09/2 ＝ 2.545となる。この値からz値を計算する。

　z ＝ (r+0.5-ur)/σr ＝ (10+0.5-13)/2.545 ＝ -0.982

標準正規分布表より、P ＝ 0.3270＞0.05 となる。P＞0.05となるので帰無仮説を棄却できない。よって、「料理Aと料理Bのおいしさに差がある」とはいえない。