役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 統計学 ＞ Bartlett(バートレット)検定

Bartlett(バートレット)検定

 

　Bartlett検定
Bartlett検定は「分散が均一であるかどうか」を検定する。独立多群や関連多群で分散分析(一元配置分散分析法、二元配置分散分析法)をするとき、分散が均一でないといけない。

 

もし、Bartlett検定によって分散が均一でないと判断されたら、分散分析では検定しない方が良い。分散が均一でないならKruskal-Wallis検定やFriedman検定を行う。

 

	測定値	データ数	分散
A1	○○○	n1	s12
A2	○○○○○	n2	s22
Ak	○○○○	nk	sk2
		N

 

n=データ数、s²=分散、k=群数

 

・仮説の設定
帰無仮説(H₀)：「各群の分散は均一である」と仮定する。(分散に差はない)
対立仮説(H₁)：「各群の分散は均一でない」と仮定する。(分散に差がある)

 

・確率を求める
統計量を求めるには、まず分散がどれくらい偏っているかを表す偏り度Mを求める。Mは次の式によって求めることができる。

 

　

 

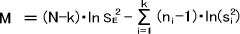
このときのs_E²は郡内変動を表す分散であり、次の式によって求めることができる。

 

　

 

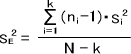
Mを求めたら、今度はデータ数の補正係数Cを求める。

 

　

 

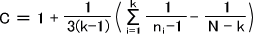
MとCを使い、次の式で偏りを標準化させることで統計量X²を求める。

 

　

 

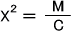
このとき、自由度df=k-1のX²分布に従うので、X²分布表よりX²_αを求めて判断する。

 

・判定
X²≦X²_αのとき、P≧αとなり帰無仮説を棄却できない　→　各群の分散は均一である
X²＞X²_αのとき、P＜αとなり帰無仮説を棄却できる　→　各群の分散は均一でない

 

………………………………………………………………………………………………………………

 

　例題
下の表のデータについて、分散は均一であるかを検定せよ。

 

	測定値	データ数	分散
A1	○○○	3	10
A2	○○○○○	5	19
A3	○○○○	4	8

(注：このデータは便宜的に作ったもので、実際のデータではない)

 

帰無仮説(H₀)：各群の分散は均一である
対立仮説(H₁)：各群の分散は均一でない

 

・計算
まず、郡内変動の分散を求めないといけない。データ数=12、群数k=3

 

　

 

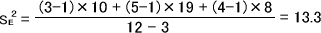
郡内変動の分散値を求めたら、偏り度Mを計算する。

 

　

 

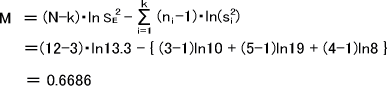
補正係数Cは次のように計算できる。

 

　

 

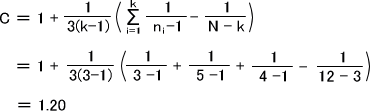
このとき、統計量はMとCを使って次の式で求める。

 

　

 

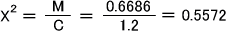
自由度df=k-1=3-1=2のX²分布に従うので、X²分布表よりX²_0.05=5.99となる。

 

X²値＜X²_0.05なので、P＞0.05となり帰無仮説を棄却できない。つまり、「各群の分散は均一でない」とはいえない。