役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 物理化学 ＞ 物質の反応速度

物質の反応速度

 

　反応速度
医薬品などの場合、時間が経過すれば次第に分解していき効果が薄くなることがある。このとき、どれくらいの速度で分解していくかを知ることができれば、医薬品の有効時間を知ることができる。もちろん、医薬品の分解以外にも化学物質同士の反応など多くの分野で利用することができる。

 

いま、A薬物が反応してPに変化するとする。このときの速度は次のように表すことができる。

 

　v = k[A]^X　(A → P)

 

このときのkは速度定数で、Xには0,1,2などの反応次数が入る。

 

　一次反応　A→P
反応次数が1の場合が一次反応である。つまり、この反応は次の式に従う。

 

　v = kC

 

Cは濃度のことである。つまり、一次反応の速度は濃度Cに依存する。

 

また、薬物の初濃度をC₀、反応した後の濃度をC、経過時間をt,速度定数をkとすると次の式によって表わすことができる。

 

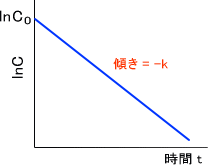
　lnC - lnC₀ = ln(C/C₀) = -kt

 

一次反応では、濃度の対数を取ってプロットすると直線関係を得ることができる。

 

　

 

多分、式を見ただけでは理解しにくいと思うので、例題を出したいと思う。

 

……………………………………………………………………………………………………………

 

問
一次反応で分解する薬物があるとする。この薬物は残存率が90％になるまで有効である。10(w/v％)の薬物が、分解速度定数k=0.050(h^-1)に従って分解するとき、薬物の有効時間は何時間か？

 

 

解答
最初の濃度C₀=10、速度定数k=0.050である。残存率が90％になるまで有効なのでC=10×0.9=9.0(w/v％)である。これを代入すると下の式になる。

 

　ln(9/10) = -0.05×t

 

これを解くと、t=2.1となる。つまり、この薬物の有効時間は2.1時間である。

 

……………………………………………………………………………………………………………

 

一次反応の場合、半減期は初濃度に依存しない。半減期とは濃度が初濃度の半分となるときの時間である。濃度が最初の半分となるので、C=1/2C₀を代入する。このとき、次の式のようになる。

 

　lnC - lnC₀

 

　= ln(1/2C₀) - lnC₀

 

　= ln(1/2C₀÷C₀)

 

　= ln(1/2)

 

　= -ln2 = -kt

 

よって、半減期t_1/2は次の式によって表わされる。

 

　t_1/2 = ln2/k ≒ 0.693/k　(ln2≒0.693)

 

　二次反応　A B→P
反応次数が2なので、次の式に従う。

 

　v = kC²

 

このとき、一次反応の時と同じように初濃度をC₀、反応した後の濃度をC、経過時間をtとすると次の式によって表わすことができる。

 

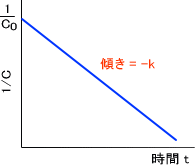
　1/C - 1/C₀ = kt

 

つまり、二次反応では濃度の逆数を取ってプロットすれば直線関係となる。

 

　

 

　零次反応　A→P
反応次数が0なので、次の式に従う。

 

　v = k

 

このとき、初濃度をC₀、反応した後の濃度をC、経過時間をtとすると次の式によって表わすことができる。

 

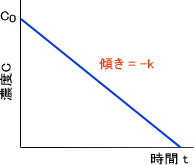
　C = C₀ -kt

 

つまり、濃度は時間とともに直線的に減少するのである。

 

　

 

それでは、零次反応,一次反応,二次反応で薬物の反応がどのように違うかを検証したいと思う。

 

……………………………………………………………………………………………………………

 

問
薬物Aの初濃度をC₀としたとき、1時間後にはAの濃度が半分(C₀/2)になった。これより、さらに1時間経過した場合、Aの濃度はいくらになるか。零次反応、一次反応、二次反応に分けて計算しなさい。

 

 

解答
・零次反応
零次反応の場合薬物の濃度は時間とともに直線的に減少する。つまり、1時間で濃度が半分になったのだから、もう1時間経過すれば濃度は0となる。

 

　答：0

 

・一次反応
C=C₀/2,t=1を代入して計算すると、k=ln2となる。

 

次に、k=ln2,t=2を代入して計算すると次のようになる。

 

　-kt

 

　= -ln2×2

 

　= -ln2²

 

　= -ln4

 

　= ln(1/4) = ln(C/C₀)

 

よって、C = C₀/4であると分かる。

 

　答：C₀/4

 

一次反応の場合、さらに1時間経過すると濃度は1/8、さらに1経過すると濃度は1/16と変化していく。

 

・二次反応
C=C₀/2,t=1を代入して計算すると、k=1/C₀となる。

 

次に、k=1/C₀,t=2を代入して計算すると次のようになる。

 

　kt

 

　= (1/C₀)×2

 

　= 2/C₀ = 1/C - 1/C₀

 

これを計算すると3/C₀ = 1/C となるので、C = C₀/3であると分かる。

 

　答：C₀/3

 

二次反応の場合、さらに1時間経過すると濃度は1/4、さらに1経過すると濃度は1/5と変化していく。

 

……………………………………………………………………………………………………………

 

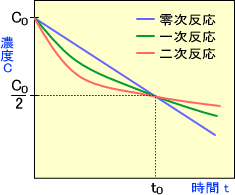
縦軸に濃度C、横軸に時間tを取ったとき、零次反応,一次反応,二次反応でそれぞれ下のような線を描く。

 

　

 

　擬零次反応
一次反応で分解する薬物であっても、零次反応で分解するように振る舞うことがある。これが擬零次反応である。この擬零次反応は、懸濁液中で起こる。

 

懸濁液ということは、いつも飽和している状態ということである。たとえ溶媒に溶けている薬物が分解したとしても、溶解していない溶液中で浮遊している成分が溶けるので濃度が変わらない。

 

　

 

懸濁液中で一次反応に従って分解していく薬物があるとする。溶解している薬物の濃度を[A]₀とすると、下のような式が成り立つ。

 

　v = k・[A]₀　([A]₀の値は一定)

 

このとき、[A]₀の値は一定なので懸濁液中で一次反応に従って分解する薬物は、零次反応で分解していくことになる。

 

分解するのは溶液中に溶けている薬物であって、懸濁液中で浮遊している薬物は分解しないと考える。なお、懸濁液として浮遊していた薬物が全て溶解してしまった後は一次反応に従って分解されていく。

 

……………………………………………………………………………………………………………

 

問
100ml中に50g含み、一次反応で分解する薬物を懸濁液で調整したとする。この薬物は残存率が90％になるまで有効である。分解速度定数k=0.050 (h^-1)に従って分解するとき、薬物の有効時間は何時間か。ただし、この薬物の溶解度は5.0 (w/v％)である。

 

 

解答
この薬物の溶解度は5.0 (w/v％)なので、100×0.05=5.0g分だけ溶液に溶けていることになる。つまり、全体の50gの薬物のうち、5gは溶解して45gは懸濁液として溶解せずに浮遊している。

 

溶解している薬物の濃度は5.0g/100mlなので、[A]₀＝5.0である。速度定数k=0.050(h^-1)なので、これらの数値を代入して求める。

 

　v = k・[A]₀

 

　　 = 0.050 × 5.0

 

　　 = 0.25(g/h)

 

また、この薬物は残存率が90％になるまで有効なのである。逆にいえば10％以上分解するまで有効であり、50×0.1=5.0g以上分解しなければよい。

 

　5/t = 0.25

 

　t = 5/0.25

 

　t = 20(h)

 

よって、この薬物の有効時間は20時間である。

 

……………………………………………………………………………………………………………

 

　擬一次反応
二次反応であるが、一次反応のように振る舞う場合を擬一次反応という。これは、薬物Aが水と反応するときに起こる。このときの速度式は次のように表わされる。

 

　v = k[A][H₂O]

 

このとき、水の量は大過剰なので少々反応しても濃度は変わらない。つまり、水の量は一定であるとみなすことができる。反応速度は薬物Aの濃度のみに依存するため、この反応は一次反応のように振る舞うのである。