量子化学
光の粒子性
光は真空中では一定の速度である。光の速度cと波長λと振動数ν(ニュー)で次のような関係がある。
c ＝νλ
光には波としての性質を示す波動性と粒子としての性質を示す粒子性の両方の性質がある。光が波の性質をもっていることは回折現象などで説明がされる。
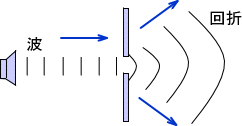
昔は「光＝波」というのが常識であった。しかし、それでは説明がつかない現象が発見された。それが光電効果である。
光を粒子として考えるとそのエネルギーは次のようになる。
E ＝ hν ＝ hc/λ
これを見ると、光のエネルギーは振動数νに比例しているのが分かる。なお、hはプランク定数と呼ばれる普遍的な定数である。
プランク定数 h＝6.63×10-34(J・s)
光電効果
金属に紫外線などの波長の短い光を照射すると、金属の表面から電子が飛び出す。これが光電効果であり、飛び出した電子を光電子という。このような現象により、光が粒子としての性質を帯びるのではと考えられた。
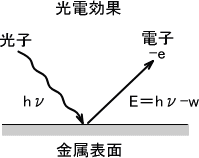
このときの光のエネルギーhνをもつ光子が金属から電子を飛び出させるエネルギーをW(仕事関数)とすると、光電子の運動エネルギーEは次のように表す。
E ＝hν - W
hν (J)：光子のエネルギー W (J)：仕事関数
光電効果には
・ある特定の波長よりも長い波長の光を照射するとき、いくら強い光をあてても光電効果は見られない
・光電効果が起こる波長なら、強い光をあてるほど単位時間に金属から飛び出す光電子の量が多い
という特徴がある。
コンプトン効果
光電効果によって「光が粒子性をもつ」と証明されているが、コンプトン効果によっても証明されている。
エネルギーhνをもつX線が電子に衝突しようとする。電子にX線が衝突すると静止していた電子は一定の速度で跳ね飛ばされ、運動エネルギーをもつようになる。衝突したX線は、電子に運動エネルギーを与えた分だけX線自体のエネルギーが減少する。そのためX線の振動数はνからν´に変化し、波長が長くなってしまう。
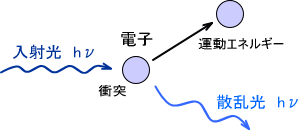
この現象がコンプトン効果(コンプトン散乱)である。なお、この現象では運動量保存の法則が成り立っている。
水素原子のスペクトル
水素や酸素などの気体を放電管に入れ低圧で高電圧をかけて放電すると、特有の光を出す。この光をプリズムなどで分光すると線スペクトルが見られる。このスペクトルはその気体特有の波長の光として表れる。
バルマーは水素原子の線スペクトルの波長に次のような関係を見つけた。
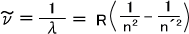
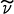は波数といいλの逆数である。Rはリュードベリ定数と呼ばれる定数である。
リュードベリ定数 R＝109678 (cm-1)
電子の波動性
光は波と考えられていたが、実は粒子としての性質を持つことが証明された。それでは「光に粒子としての性質があるなら、粒子にも実は波としての性質があるのではないか」とド・ブロイは考えた。
この波動性をもつ粒子をド・ブロイ波(物質波)という。運動量pの物質はλ＝ h/p ＝ h/mv の物質波として振舞う。
原子や電子レベルの物質は粒子だけでなく波としての性質を持ち、光は波だけでなく粒子としての性質を持つ。これを波動-粒子の二重性という。
不確定性原理
野球のボールのように大きい物質では速度(運動量)を正確に測ることができる。これは、野球のボールの大きさでは波動性がほとんどなく、粒子としてだけの性質が現れているからである。
しかし、これが粒子のようなミクロの世界では波動性も現れるため、ある位置での速度(運動量)を簡単に測定することはできない。位置の不確かさを⊿q、運動量の不確かさを⊿pとすると次の式の関係が成り立つ。
⊿q・⊿p ≧ h/4π
この関係をハイゼンベルクの不確定性原理という。それでは、実際に計算して理解してみようと思う。
①「1辺が1mの立方体の箱の中にある1kgの重りの速度」と②「1辺が1nmの立方体の箱の中にある電子の速度」のそれぞれの不確かさを出したいと思う。(電子の重さは9.109×10-31とする)
運動量pはp ＝ mvなので、⊿p ＝ m⊿vである。つまり、速さは次式で求められる。
⊿v ≧ h/4πm⊿q
これで計算すると、それぞれ①は5.8×10-35(mls)、②は5.3×104(m/s)と計算できる。この結果を見ると、電子の速度の不確かさの方が著しく大きいということが分かる。
現在の量子力学は不確定性原理を受け入れた上で成り立っている。そして、この不確定性原理が量子力学特有の確率論的なイメージを与える。
スポンサードリンク
カテゴリー
スポンサードリンク