役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 物理化学 ＞ 光の性質

光の性質

 

　光の強度
光の強度がI₀の単色光が、ある特定の溶媒を通過したとき、出てきた光の強度をIとする。このとき透過度tをI/I₀とする。透過率Tは T ＝ I/I₀×100 ＝ 100t とする。溶媒の濃度をc、セルの長さをlとする。

 

　

 

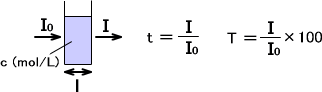
どれくらい光を吸収したかを表すには吸光度Aで表す。

 

　

 

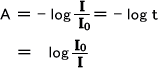
吸光度Aは濃度一定では光が透過するセルの長さlに比例する。これをランベルトの法則という。また、吸光度Aは濃度cに比例する。これをベールの法則という。この二つの法則を組み合わせると、吸光度Aを次のように表すことができる。

 

　A ＝ εcl

 

この関係をランベルト・ベールの法則という。このとき、cを1mol/Lの溶液、lを1cmにしたときの吸光度をモル吸光係数εという。

 

　蛍光、りん光
原子内の電子は光のエネルギーを吸収すると、電子が高エネルギー状態になるのでよりエネルギーの高い軌道に移る。この原子内の電子軌道が変化することを電子遷移と呼び、電子が高エネルギー状態のときを励起状態と呼ぶ。

 

エネルギーを吸収した電子はエネルギーを放出して安定になろうとする。電子がエネルギーを放出し、安定な低エネルギー状態になるときに光が放出される。この低エネルギー状態を基底状態と呼ぶ。このとき、電子は元の軌道に戻る。

 

原子核は電子に比べて非常に重たいので、電子遷移は核が対応できないほど速く起こる。これをフランク・コンドン原理という。光を吸収することで基底状態から励起状態になるとき、電子遷移は核配置が一定のまま起こる。つまり、光を吸収した分子の核配置は基底状態のときの核配置と同じである。

 

核配置が一定のまま振動緩和が起こり、同じ励起状態の中でもさらにエネルギーが低い状態になる。つまり、振動が緩和されることでエネルギーが減少する。

 

そこから電子は基底状態に向かって蛍光発光遷移が起こる(蛍光発光)。吸収したエネルギーよりも蛍光になるエネルギーの方が小さいため、蛍光極大波長は励起極大波長よりも長波長側にある。

 

　

 

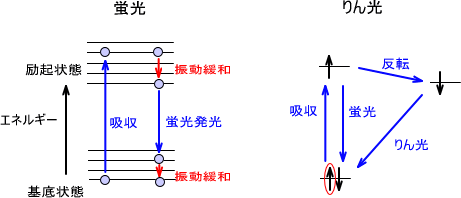
蛍光に対しりん光は寿命がはるかに長い。あたりまえだが蛍光灯の電気を消すと一瞬で暗くなってしまう。しかし、りん光を発光する物質は回りが暗くなった後もぼんやりと発光し続ける。

 

りん光は励起されるまでは蛍光と同じである。りん光となるには励起された後、スピンが反転する。これが元の基底状態に戻るには、もう一回スピンを反転させないといけないので時間がかかってしまう。そのため光が長く続く。

 

　散乱
光は波動である。光の波長がある物質の大きさよりも大きいとその間をすり抜けてしまう。しかし、光の波長が粒子と同じくらいやそれ以下であると散乱する。

 

例としてはよくボートが使われる。水の上にボートが浮かんでいるとする。ここに大きい波が来たとしても、ボートは上下に揺れるだけである。しかし、小さい波であるとボートの縁で波が反射してしまい、いろいろな方向に散乱する。

 

空が青いことや夕焼けが赤く見えるのもこれで説明することができる。可視光の波長は約400～700nmであり、赤色→青色になるに従って波長は短くなる。波長が短い方が空気中の粒子によって散乱されやすい。つまり、青色は空気中の粒子によって散乱されやすいのである。空が青いのは大気中の分子によって散乱された青色が目に入るためである。

 

また、波長の長い赤色は可視光の中では散乱されにくい透過光である。そのため、夕焼けは青色などの光が排除された赤色が見えるのである。

 

　

 

また、散乱には散乱後に振動数(エネルギー)が変化する散乱とそうでない散乱がある。入射光と同じエネルギーで散乱するのをレイリー散乱と呼び、入射光と異なるエネルギーで散乱するのをラマン散乱という。ラマン散乱の中で、散乱光のエネルギーが低い光(振動数↓、-⊿ν)をストークス光と呼び、散乱光のエネルギーが高い光(振動数↑、 ⊿ν)を反ストークス光と呼ぶ。

 

　

 

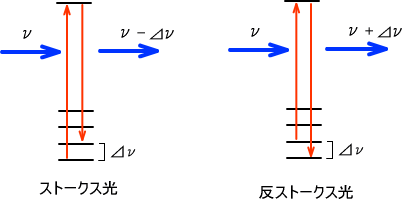
ラマン散乱による振動数の違いを測定するのがラマンスペクトルである。

 

　偏光
光は様々な方向に振動している。この振動は進行方向に対して垂直である。偏光とは特定の方向に振動している光である。

 

もし特定の振動方向だけの光を取り出すと、光の振動方向は全て同じになる。このように特定の偏光を取り出すことのできる物質を偏光子といい、取り出された特定の振動だけをする光を平面偏光という。また、この偏光の振動面を偏光面という。

 

　

 

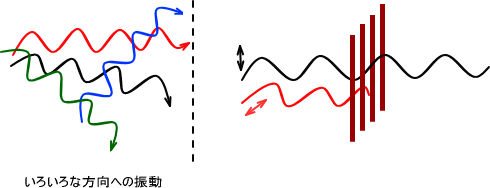
上の図のように光は縦、横、斜めなどいろいろな方向に振動している。今ここに、縦方向の振動と横方向の振動をしている二つの波が来るとする。そこに縦方向の波のみを通過させるように偏光板を置くと、横方向の波はカットされて縦方向の波だけが通過する。

 

二つの偏光板を用意して両方とも同じ方向の波が通過できるようにすると、偏光された光はそのまま二つ目の偏光板も通過する。しかし、二つ目の偏光板を90°回転させると光を完全に遮断される。

 

　

 

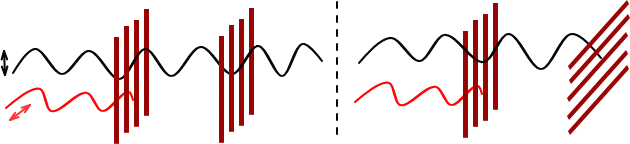
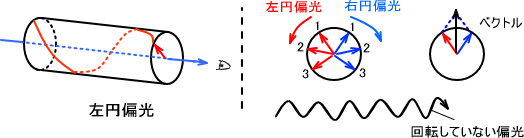
この偏光には回転しながら進行する光があり、そのような光を円偏光という。この円偏光は光が来る方向から見て、時計回りに回転するのが右円偏光であり反時計回りに回転するのが左円偏光である。

 

ところで、右にも左にも回転していない偏光(平面偏光)はどのように考えることができるであろうか。これは「全く同じ振動と周期で進行している右円偏光と左円偏光のベクトルの和」と考えるができる。

 

　

 

　旋光性
平面偏光でも、特定の物質と相互作用をすると右や左に回転することがある。この現象を旋光といい、そのとき回転した角度を旋光度という。

 

前述の通り、平面偏光は「全く同じ右円偏光と左円偏光が合わさったもの」と考えることができる。このとき、ある物質の右円偏光と左円偏光の進む速さが異なると、透過光が曲がってしまう。

 

例えば、左円偏光よりも右円偏光の方が流れが速いと合成ベクトルは右に回転する。つまり透過した後の平面偏光は右に曲がっているのである。

 

　

 

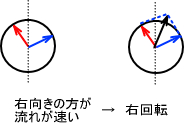
上の例で示したような偏光面を右に回転させる物質を右旋性物質という。また、左に回転させる物質を左旋性物質という。それぞれ右旋光を記号で d- 、( )- と表記し、左旋光を 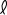- 、(-)- と表記する。

 

旋光を起こす物質の旋光度(α)は、溶液の濃度(c)、透過距離(l)に比例し、温度(t)、平面偏光の波長(λ)に依存している。このときの溶液の旋光性を比旋光度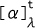で表すことができる。比旋光度を次式のように定義する。

 

　

 

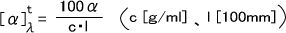
上の式より、比旋光度は「濃度cの溶液が示す、光路100mmあたりの旋光度」であると理解することができる。

 

　結晶構造と回折現象
・ブラッグの式
結晶にX線を照射すると各層で散乱する。入射光と同波長の光が散乱するとき、この散乱をトムソン散乱という。各層で散乱したX線が強めあうには各層の反射光が同位相でなくてはならない。この関係は次のブラッグの式で表すことができる。

 

　2d sinθ ＝ nλ (λ＝1,2,3…)

 

ブラッグの式は次のように証明できる。

 

　

 

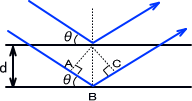
上の図のように光が反射するとき、二つの光が進む距離の長さの差はABとBCの長さの違いである。ABの距離はdsinθでだすことができ、ABとBCの距離を足したものは2d
sinθである。

 

二つの光が互いに強めあうには、この光路差が波長の整数倍になればいいのでnλ (n＝1,2,3…)となる。

 

結晶は三次元格子であり、回折点と反射面にミラー指数(h,k,l)を付けて解析する。ミラー指数は(h,k,l)で表すことができ、結晶格子での3本の軸(a,b,c)がどのような方向かを示している。

 

　

 

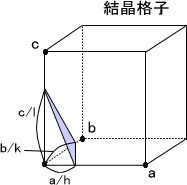
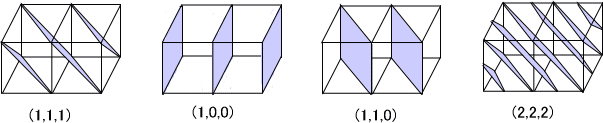
ミラー指数とは結晶構造の表記の仕方であり、(h,k,l)はそれぞれ(a軸、b軸、c軸)に対応し、a/h、b/k、c/lで表せる。例えば、ミラー指数が(1,1,1)ならば結晶格子は(a,b,c)となる。(1,0,0)なら結晶格子は(a,∞,∞)、(1,1,0)なら(a,b,∞)となり、(2,2,2)なら(a/2,b,2,c/2)となる。指数l＝0というのはc軸との切片が無限の場合であり、c軸に平行になる。

 

　

 

・粉末X線回折法
粉末試料にX線を照射すると、結晶の格子面はいろいろな方向に向いているためX線回折はあらゆる方向に生じる。

 

　

 

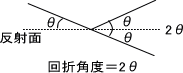
回折X線は回折角度が2θになる。粉末X線回折法は結晶、結晶多型などの同定に適用される。