役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 薬剤・薬物動態学 ＞ ファーマコキネティクス（PK：薬物動態）

ファーマコキネティクス（PK：薬物動態）

 

薬を経口投与した場合、薬の血中濃度が上がっていった後、血中濃度が下がる図を描くことができる。ただし、薬物動態を考える上で「薬の吸収過程」と「消失されていく過程」の二つを考えないといけないため、とても複雑になる。

 

そこで、薬物動態を分かりやすく考えるために「薬の消失過程」だけを考えるようにする。具体的には、薬の経口投与ではなくて「注射による静脈内投与」を考える。

 

薬を注射によって静脈内投与した場合、薬は血液を介してすぐに全身を巡りる。そのため、静脈内投与では「薬を投与した瞬間に薬物が全身に分布する」と考える。この時、薬物の血中濃度推移は下図のようになる。

 

　

 

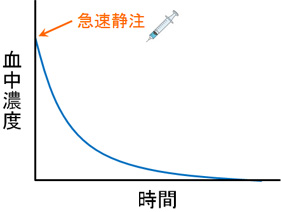
当然ながら、静脈内投与では薬の吸収過程が存在しない。そのため、薬の消失過程だけを考えれば良い。さらにこの時、「薬を投与した瞬間＝血中濃度が最も高くなっている点」であることも分かる。

 

　消失速度定数
薬物の消失過程を考える場合、消失速度定数（k_el）を考える必要がある。ただし、そこまで難しく考える必要はない。

 

当然ながら、薬によって体の中から消失していく速度は異なる。素早く消失していく種類の薬があれば、代謝・排泄に時間がかかる薬物もある。そのため、「どれくらいの速度で体内から薬物が消失していくか」を表すパラメーターとして消失速度定数（k_el）が必要になる。

 

つまり、消失速度定数は「その薬がどれだけの速度で消失していくかを表す定数である」というだけである。

 

　薬物の単回投与モデル
　・静脈内投与（急速静注）
薬物を静脈内投与したとき、その薬物は消失過程だけを考えれば良い。この時、血中濃度は次の式によって表わされる。

 

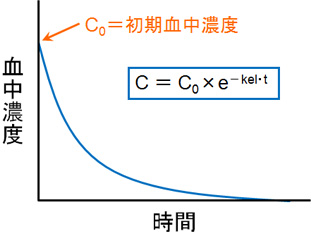
　C ＝ C₀ × e^－kel・t

 

　※「C＝その時点での血中濃度、C₀＝初期血中濃度、k_el＝消失速度定数、t＝経過時間」

 

注射によって投与しているため、前述の通り注射直後の血中濃度は一番高い値（C₀を示す。この値から、時間が経つに従って血中濃度が減少していくようになる。

 

なお、この式は覚えないとどうしようもない。「薬物は主にこの式に従って消失していく」と割り切るしかないのである。そのため実際に薬物動態を計算する時、この式だけは諦めて覚えて欲しい。

 

ただし、薬物動態の概念だけを理解したいのであれば覚えなくても問題ない。なお、静注投与後の血中濃度は次のようなグラフを描く。

 

　

 

ただし、上のグラフは曲線であるため、このグラフを使って薬物動態に必要な公式を導き出すのは難しい。そこで、このグラフを直線のグラフに変換する。この方法として、「両辺の自然対数を取る」という事がある。

 

この時、「C ＝ C₀ × e^－kel・t」の自然対数を取ると、以下のような式へと変換される。

 

　lnC ＝ －k_el・t ＋ lnC₀

 

高校レベルの数学を思い出す必要はないが、対数の概念さえ思い出すことができれば良い。そしてこの式であると、以下のようなグラフになる。

 

　

 

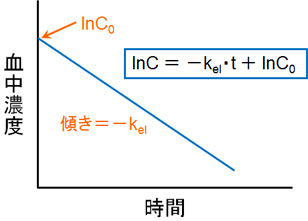
中学生レベルの数学を理解しておけば、この自然対数を取った式の意味を理解することができる。この式の中で変化していく値は時間（t）だけである。「時間（t）＝1分後、10分後、1時間後」といった具合に変わっていく。

 

消失速度定数（k_el）は「どれだけの速さで薬が消失していくかを表す定数」であるため、この値は変わらない。また、投与する薬物量は決まっているため、初期血中濃度（C₀）の値も既に決定されている。

 

つまり、「Y ＝ aX ＋ b」の式と同じになる。今回の場合、「a ＝ －k_el」、「X ＝ t」、「b ＝ lnC₀」に置き換えただけであることが分かる。そのため、このグラフの切片はlnC₀であり、直線の傾きは－k_elとなる。このように、「グラフの傾きから消失速度k_el」、「切片から初期血中濃度C₀」をそれぞれ導き出すことができる。

 

　・消失速度定数（k_el）と半減期（t_1/2）
半減期は「血中濃度が半分になるまでの時間」を指す。この時、血中濃度は「lnC ＝ －k_el・t ＋ lnC₀」の式で表される。そして、薬物濃度が半分になるまで時間が経過したとすると、血中濃度は投与直後の濃度（C₀）の半分である（1/2C₀）になっていることが分かる。

 

そのため、血中濃度を計算する式の中で「C＝1/2C₀」、「t＝t_1/2」を代入する。すると、下のような式になる。

 

　

 

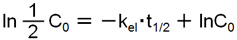
この対数を計算すると、以下のような計算式になる。

 

　

 

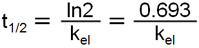
このように、半減期から消失速度定数を計算することができる。なお、半減期の単位が時間（minやh）であることから、消失速度定数の単位は（/minや/h）となる。

 

　・点滴静注
これまでの話は注射として静脈内投与した場合であった。この時、投与直後が最も血中濃度が高く、その後は時間経過と共に血中濃度は減っていく。

 

それに対して、今度は点滴による薬物投与を考える。点滴では少しずつ薬を投与していく。そのため、点滴によって薬物投与を行った場合、時間が経つに従って血中薬物濃度は定常状態に近づいていくようになる。このときのグラフは下のようになる。

 

　

 

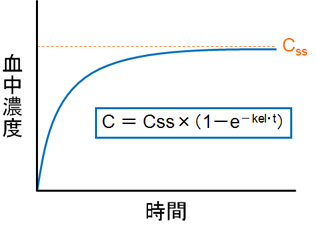
また、点滴静注のときの血中濃度は次の式によって表わすことができる。一見複雑に見えるが、よく考えると当たり前のことを書いてある式となる。

 

　C ＝ Css×(1－e^－kel・t)

 

Cssとは定常状態に達したときの薬物血中濃度のことである。つまり、最も高い値を示す血中濃度のことを指す。最高血中濃度ということから考えると、「Css」も「C₀」も考え方からしたら何も変わりはない。

 

ただし、この式は別に覚えなくても簡単に導き出すことができる。下に「注射による急速静注の場合」と「点滴静注の場合」による血中濃度推移のグラフを示す。

 

　

 

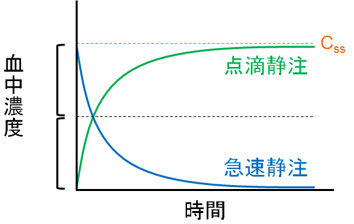
見て分かるとおり、急速静注と点滴静注の血中濃度推移はそれぞれ対称となっている。この時、前述した通り急速静注の場合の式は「C ＝ C₀ × e^－kel・t」で表される。

 

それに対し、点滴静注の場合は100％の数字を表す「1」から「e^－kel・t」の差を取るようにして、「C ＝ Css×(1－e^－kel・t)」としただけである。

 

なお、Cssは定常状態のときの血中濃度であるため、急速静注でのC₀の値と同じになる。そのため、「Css＝C₀」と考えれば良い。

 

　薬物の連続投与
薬を投与した時、その薬は体内で代謝・排泄されていく。これによって血中濃度が下がっていく。この時、半減期の長い薬（体内から消失していく速度が遅い薬）の場合であると、徐々に血中薬物濃度が上がっていく。

 

　

 

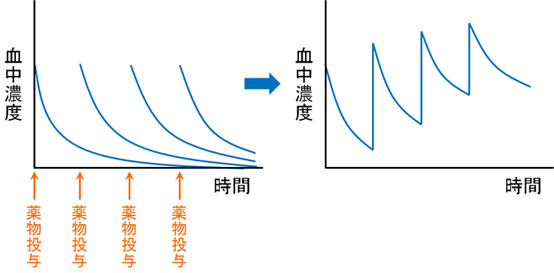
薬物を投与したごとの血中濃度推移を見てみると、上の左図のようになる。ただし、それぞれの薬物濃度を足し合わせたものが血中濃度となるため、実際には上の右図のようになる。

 

そして、薬物投与を継続していくと、ある時点で薬の血中濃度推移が一定になる。この時が定常状態であり、「薬の投与速度＝薬の消失速度」となる。なお、この定常状態は静脈内投与であっても経口投与であっても起こる。