役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 薬剤・薬物動態学 ＞ 薬物の単回投与モデル

薬物の単回投与モデル

 

　薬物の単回投与モデル
薬物を注射で投与したときにその薬物が一次速度で消失する場合、血中濃度は次の式によって表される。

 

　C ＝ C₀×e^-kel・t

 

※「C＝血中濃度、C₀＝初期血中濃度、kel＝消失速度、t＝経過時間」

 

注射によって投与しているので、注射直後の血中濃度は一番高い値(C₀)を示す。この値から、時間がたつに従って血中濃度が減少していくのである。

 

なお、この式は覚えないとどうしようもない。そのため、「一次速度で消失する薬物はこの式に従って減少する」と割り切るしかないのである。

 

①静脈内投与(急速静注)
前述のとおり、注射などによって静脈内投与を行った場合、時間が経つに従って血中濃度が減少してくる。このとき、次のようなグラフを描くことができる。

 

　

 

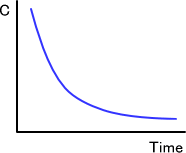
ただし、このグラフからでは読み取れる情報は限られてくる。そのため、「C ＝ C₀×e^-kel・t」の式の両辺で対数(log)を取るとする。すると、次の式を導き出すことができる。

 

　logC ＝ logC₀ － (kel/2.303)・t

 

両辺の対数(log)を取った式なので、この式は片対数グラフにプロットした場合と適応させることができる。そして、それぞれの経過時間に対する血中濃度を片対数グラフにプロットすると次のようなグラフを描くことができる。

 

　

 

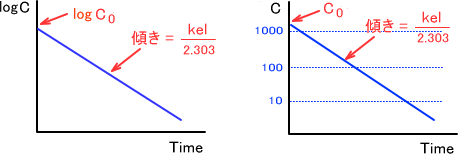
※「左のグラフ」は普通のグラフにプロットしたものである。そのため、それぞれの時間に対応するlogCの値をプロットしている。しかし、「右のグラフ」は片対数グラフであるため、そのままの値をプロットするだけで勝手に対数表になってくれる。

 

上記の式を見て分かるとおり、グラフでの傾きが「kel/2.303」となっている。また、切片がC₀となっていることが分かる。

 

何が言いたいかというと、「グラフの傾きから消失速度kel」「切片から初期血中濃度C₀」をそれぞれ導き出すことができるということである。

 

②点滴静注
点滴によって薬物投与を行った場合、時間が経つに従って血中薬物濃度は定常状態に近づいてくる。このときのグラフは下のようになる。

 

　

 

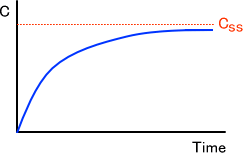
また、点滴静注のときの血中濃度は次の式によって表わすことができる。なお、Cssとは定常状態に達したときの薬物血中濃度のことである。つまり、最も高い値を示す血中濃度のことである。最高血中濃度ということから考えると、「Css」も「C₀」も考え方からしたら、何も変わりはない。

 

　C ＝ Css×(1－e^-kel・t) ＝ k₀/CLtot×(1－e^-kel・t)
※Css ＝ k₀/CLtot

 

ただし、この式は別に覚えなくても簡単に導き出すことができる。下に「注射による急速静注の場合」と「点滴静注の場合」による血中濃度推移のグラフを示す。

 

　

 

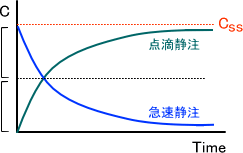
見て分かるとおり、急速静注と点滴静注の血中濃度推移はそれぞれ対称となっている。

 

そのため、急速静注の場合の式は「C ＝ C₀×e^-kel・t」であるが、点滴静注の場合は100％の数字を表す「1」から「e^-kel・t」の差を取るようにして、「C ＝ Css×(1－e^-kel・t)」としただけである。

 

なお、Cssは定常状態のときの血中濃度であるため、急速静注でのC₀の値と同じである。そのため、「Css＝C₀」と考えればよい。

 

③点滴静注後の血中濃度推移
点滴静注後は一次速度に従って血中薬物濃度が減少していく。つまり、点滴静注終了直後の薬物濃度をC₀とし、終了直後からどれだけ時間が経過したかによって簡単に導き出すことができる。

 

　

 

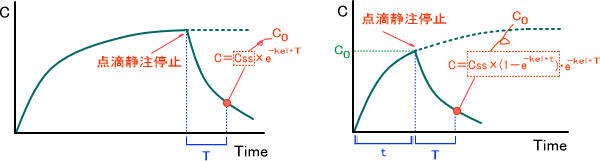
定常状態に達している状態からの点滴終了後血中濃度を調べたいのなら「C ＝ Css×e^-kel・T」で出すことができる。また、定常状態に達する前での点滴終了後血中濃度を調べたいのなら「C ＝ Css×(1－e^-kel・t)・e^-kel・T」で出すことができる。

 

※「定常状態に達している状態」からでも「C ＝ Css×(1－e^-kel・t)・e^-kel・T」で導き出すことができる。

 

なお、これらは全て「C ＝ C₀×e^-kel・t」の式と全く同じと考えることができる。ただ単に、どの時点で点滴静注を終了するかによって、C₀の値が異なってくるというだけである。