役に立つ薬の情報～専門薬学＞分析化学＞pHの計算(弱酸・弱塩基溶液)
役に立つ薬の情報～専門薬学 サイトマップ


　　　pHの計算(弱酸・弱塩基溶液)
　酸塩基の定義
Brφunsted・Lowryの定義
Brφunsted・Lowryの説では、「酸とはプロトンを放出し得るプロトン供与体であり、塩基とはプロトンを受け取り得るプロトン受容体である」と定義している。

Lewisの定義
Lewisの理論では酸と塩基の定義をBrφunsted・Lowryの説よりさらに広義なものとしている。Brφunsted・Lowryではプロトンの移動としているが、Lewisでは電子の受け渡しで定義している。これによると、「酸とは電子対を受け取り得るものであり、塩基とは電子対を与え得るもの」と定義している。

　弱酸・弱塩基溶液
弱酸の一塩基酸において、濃度Caの弱酸HAでは次の式が成り立つ。

　　　

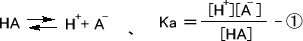
陽イオンと陰イオンの数は等しくなるので次のようになる。
　　　[H+] ＝ [A-] + [OH-]
しかし、HAが極めて弱い酸でないなら酸性を示すのでOH-は無視できるくらい小さい数となる。
　　　[H+] ＞＞ [OH-]　、　[H+] ≒ [A-] -②

酸であるHAは水溶液中で必ずHAかA-の形をとるので、
　　　Ca ＝ [HA] + [A-] -③

①に②と③をそれぞれ代入すると

　　　

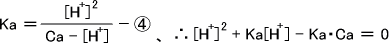
この式を[H+]について解けば溶液中の水素イオンの濃度を求めることができる。

溶液があまり希薄でない場合は弱酸の電離は小さいのでCa ＞＞ [H+] となり、Ca - [HA] ≒ Ca となる。これで④を変形すると次のようになる。

　　　

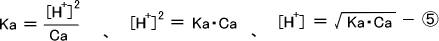
一塩基酸では[H+] ＞＞ [OH-] 、 Ca ＞＞ [H+] の場合のみ⑤の式が使用できる。ただし、⑤の式を使用する場合は得られた結果についてその仮説が妥当であったかを検証する必要がある。


例１
1.0mol/Lの酢酸(Ka ＝ 1.8×10-5)のpHを求めよ。

[H+] ＞＞ [OH-] 、 Ca ＞＞ [H+] であると仮定する。
⑤の式に代入すると 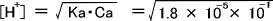となる。
これを計算して[H+] ＝ 1.34×10-3　、　pH ＝ 2.87

　検証
[H+][OH-] ＝ Kw ＝ 1.0×10-14　、　[OH-] ＝ Kw/[H+] -⑥
⑥より[OH-]を計算すると[OH-] ≒ 1×10-11
よって、[H+] ＞＞ [OH-]
また、Ca ＝ 0.10 ＞＞ 1×1.34×10-3 ＝ [H+]
となるため、この仮定は妥当であったと分かる。

例２
0.10mol/LのNH4Cl溶液のpHを求めよ。ただし、アンモニア(Kb ＝ 1.8×10-5)とする。

NH4Clは塩なので完全に電離する。

　　　

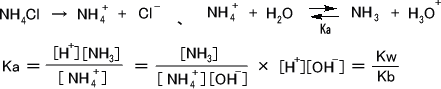
[H+] ＞＞ [OH-] 、 Ca ＞＞ [H+] であると仮定する。

　　　

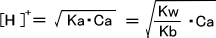
これに代入すると [H+] ＝ 7.41×10-6(mol/L) 、 pH ＝ 5.13 となる。


一酸塩基の場合も同様に求められる。
ただしpHは
　　　pKw ＝ pH + pOH 、 pH ＝ 14 - pOH から求める。