役に立つ薬の情報～専門薬学 ｜ 薬・薬学・専門薬学・薬理学など

役に立つ薬の情報～専門薬学 ＞ 統計学 ＞ Wilcoxon(ウィルコクソン)検定

Wilcoxon(ウィルコクソン)検定

 

　Wilcoxon検定(ノンパラメトリック法)
符号検定では＋の個数と－の個数を比較した。しかし、Wilcoxon検定では符号の差だけではなく、個々のデータが0の値からどれだけ離れているかも検定する。

 

例えば、下の図のように＋と－が分布しているとする。

 

　

 

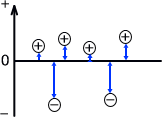
このとき、＋と－の個数を比較すると「＋が4つ」で「－が2つ」のため、＋の数の方が多い。しかし、＋の数が多いからといって「グラフは全体的に＋である」ということはよくない。

 

数値の大きさで見てみると－の方が数値が大きいため、単純に＋の個数と－の個数だけでは差を決定できないのである。

 

・仮説の設定
帰無仮説(H₀)：「2群間に差がない」と仮定する。
対立仮説(H₁)：「2群間に差がある」と仮定する。

 

・確率を求める
まず、両ペアで差dを計算する。差が0のペアを除外した後、符号を無視してdの値が小さいものから順に並べる。

 

その後、dの符号（＋と－）によって順位を分けて符号の数が少ない方の順位を足してT値とする。

 

例えば、「-1, 3, 4, -6, 8, 10のd値がある」となるとき、順位はそれぞれ「1, 2, 3, 4, 5, 6」の6つとなる。それぞれ＋と－によって分けると＋が「2,3, 5, 6番」、－が「1, 4番」となる。少ない方の符号の順位を足すのでT値は次のようになる。

 

　T ＝ 1＋4 ＝ 5

 

ただし、d値で「-2 ,4, 4, 5」などのように「4, 4」と同じ値があるときの順位は「1, 2.5, 2.5, 4」となる。「4」の順位は「2と3を足して2で割るので2.5となる。

 

それでは、「-2, 2, 2, 4, 4, 5, 6, -6」のときの順位はどうなるでしょうか。「2」の順位は(1＋2＋3)/3＝2、「4」の順位は(4＋5)/2＝4.5、「6」の順位は(7＋8)/2＝7.5となる。つまり、順位は「2,2, 2, 4. 5, 4. 5, 6, 7.5, 7.5」となる。

 

データ数nがn≦25のときはWilcoxonの検定表からT値がそれ以上極端となる確率Pを求める。

 

・判定
P≧αのとき帰無仮説を棄却できない。
P＜αのとき帰無仮説を棄却する。有意差あり。

 

………………………………………………………………………………………………………………

 

・確率を求める
それに対し、データ数nがn≦25のときは下の式から平均値と標準偏差を出してz値を出す。この式によってTの分布は近似的に正規分布する。

 

　

 

その後、標準正規分布表から確率Pを求める。

 

　例題(小標本)
A大学とB大学は毎年スポーツ種目で競い合っている。今年の12種目のインカレでの順位はそれぞれ下のようになった。この結果から、どちらかの大学の方が上回っているといえるかどうかを検定しなさい。

 

種目	a	b	c	d	e	f	g	h	i	j	k	l
A大学	3	16	4	3	4	7	1	2	3	7	10	4
B大学	5	8	7	3	5	2	7	11	10	2	3	14
競技順位の差(A-B)	-2	8	-3	0	-1	5	-6	-9	-7	5	7	-10

(注：このデータは便宜的に作ったもので、実際のデータではない)

 

帰無仮説：A大学とB大学の順位には差がない。
対立仮説：どちらかの大学の順位が、全体的に上回っている。

 

・計算
まず、符号を無視して差dを小さい方から順に並べて順位をつける。その後、dの符号（＋と－）によって順位を分ける。

 

差d -1 -2 -3 5 5 -6 7 -7 8 -9 -10 順位 1 2 3 4.5 4.5 6 7.5 7.5 9 10 11

＋ 4.5 4.5 7.5 9 － 1 2 3 6 7.5 10 11

 

＋の符号の数の方が少ないので、＋の符号の順位を足してT値とする。

 

　T値 ＝ 4.5＋4.5＋7.5＋9 ＝ 25.5

 

差が0のデータは除くので、データ数n＝12-1＝11となる。

 

n≦25なので、Wilcoxon検定表からT_0.05を求める。表を見るとn＝11のとき、P＜0.05のTの有意点は10であると分かる。

 

計算されたT値は両側確率P＜0.05となるTの有意点よりも大きい。よって、帰無仮説を棄却することができず、「どちらかの大学の順位が、全体的に上回っている」ということができない。

 

………………………………………………………………………………………………………………

 

　例題(大標本)
A大学とB大学は毎年スポーツ種目で競い合っている。今年の30種目のインカレでの順位はそれぞれ下のようになった。この結果から、どちらかの大学の方が上回っているといえるかどうかを検定しなさい。

 

種目 a b c d e f g h i j k l m n o A大学 3 16 4 2 4 7 1 2 3 7 10 4 3 3 5 B大学 5 8 7 2 5 2 7 11 10 2 3 14 2 15 13 競技順位の差(A-B) -2 8 -3 0 -1 5 -6 -9 -7 5 7 -10 1 -12 -8

種目 p q r s t u v w x y z α β γ δ A大学 3 18 2 3 7 1 3 1 8 9 5 13 4 3 13 B大学 6 6 15 6 3 17 2 5 2 11 2 2 1 9 2 競技順位の差(A-B) -3 12 -13 -3 4 -16 1 -4 6 -2 3 11 3 -6 11

(注：このデータは便宜的に作ったもので、実際のデータではない)

 

帰無仮説：A大学とB大学の順位には差がない。
対立仮説：どちらかの大学の順位が、全体的に上回っている。

 

・計算
基本的に小標本のときと同じように手順を踏んで計算すればよい。

 

符号を無視して差dを小さい方から順に並べて順位をつける。その後、dの符号（＋と－）によって順位を分ける。

 

差d 1 1 -1 -2 -2 3 3 -3 -3 -3 4 -4 5 5 6 順位 2 2 2 4.5 4.5 8 8 8 8 8 11.5 11.5 13.5 13.5 16

差d -6 -6 7 -7 8 -8 -9 -10 11 11 12 -12 -13 -16 順位 16 16 18.5 18.5 20.5 20.5 22 23 24.5 24.5 26.5 26.5 28 29

＋ 2 2 8 8 11.5 13.5 13.5 16 18.5 20.5 24.5 24.5 26.5 － 2 4.5 4.5 8 8 8 11.5 16 16 18.5 20.5 22 23 26.5 28 29

 

＋の符号の数の方が少ないので、＋の符号の順位を足してT値とする。

 

　T値 ＝ 2＋2＋8＋8＋11.5＋13.5＋13.5＋16＋18.5＋20.5＋24.5＋24.5
26.5 ＝ 189

 

差が0のデータは除くので、データ数n＝30-1＝29となる。

 

データ数が25以上なので、次の式によって平均値と標準偏差を求め、その後z値を求める。この式でTは近似的に正規分布となる。

 

　

 

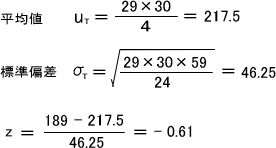
計算したZ値より、標準正規分布表から確率Pを求めるとP ＝ 0.5418＞0.05 となる。P＞0.05なので帰無仮説を棄却できない。つまり、「どちらかの大学の順位が、全体的に上回っている」ということができない。