| 役に立つ薬の情報〜専門薬学＞統計学＞X2(カイ二乗)適合度検定 | |||
 |
 サイトマップ |
||
| 役に立つ薬の情報〜専門薬学＞統計学＞X2(カイ二乗)適合度検定 | |||
|
サイトマップ |
||
X2(カイ二乗)適合度検定 |
||||||||||||||||||||||||||||||||||||||||
| X2適合度検定 X2適合度検定はデータが予測される確率(割合)の通りになっているかどうかを判定する。 例えば、サイコロを振って1の目が出る確率は普通1/6である。しかし、サイコロに細工をすればそうはいかない。このようなサイコロの目の出方が一様であるかどうかを調べるには、X2適合度検定を使う。
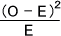
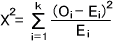
上の表で「観測度数」は実際に行って観測した数値で、「期待度数」は予測される数値である。 ・仮説の設定 帰無仮説(H0)：「観測度数と期待度数の数値は一致する」と仮定する。 対立仮説(H1)：「観測度数と期待度数には有意に差がある」と仮定する。 ・確率を求める 各セルにおいて、観測度数Oと期待度数Eとのずれは次の式によって定量化することができる。  全体の偏りは各セルで生じた偏りを全部足したものなので、次の式によって表せる。  観測度数Oiと期待度数Eiの全体のずれが偶然起こったものであるなら、ここで求めたX2値はX2に従う。ただし自由度dfは理論度数によって異なり、下のようになる。 ・一様分布のとき、df＝k-1 ・二項orポアソン分布のとき、df＝k-2 ・正規分布のとき、df＝k-3 このときのkは分類した数(セルの数)である。また一様分布とは、全ての区間を同等の値をとる分布である。 自由度を求めたらX2分布表からX2αを出す。 ・判定 X2≦X2αのとき、P≧αとなり帰無仮説を棄却できない。 X2＞X2αのとき、P＜αとなり帰無仮説を棄却する。有意差あり。 ……………………………………………………………………………………………………………… 例題 サイコロを60回振ったとき、目の出た度数は下のようになった。このとき、目の出方は一様と考えてよいか。
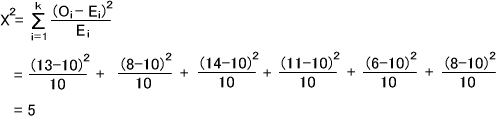
帰無仮説(H0)：サイコロの目の出方は一様である 対立仮説(H1)：サイコロの目の出方は一様でない ・計算 サイコロを60回振ったとき、「サイコロの目の出方は一様である」と考えるなら、予想される期待度数は上の表のようにそれぞれ60/6＝10となる。 後は、各セルの観測度数と期待度数の偏りを計算して足せばよい。  この分布は全ての区間を同等の値をとる一様分布であるため、自由度dfはk-1＝6-1＝5である。つまり、自由度5のX2分布に従う。 X2分布表より、X20.05＝11.07であると分かる。X2＜X20.05なので、P＞0.05となり帰無仮説を棄却できない。つまり、「サイコロの目の出方は一様である」ということができる。 つまり、この問題で示した程度のサイコロの偏りなら、実際に起こりうると判断される。   |
||||||||||||||||||||||||||||||||||||||||