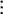2×2分割表、l×m分割表

　2×2分割表
X²適合検定ではひと続きの独立なデータとして分類した。それに対し、2×2分割表は行・列がそれぞれ二方向ある分類である。

X²適合検定で観測度数と期待度数の偏りを計算してX²値を求めたのと同じように、2×2分割表の計算でも観測度数と期待度数の偏りを計算してX²値を求める。2×2分割表では行・列での値が互いに独立かどうかを検定する。

分類	A1	A2	…	Ak
観測度数	O1	O2	…	Ok
期待度数	E2	E2	…	Ek

　↑X²適合検定

	B1	B2	合計
A1	a	b	R1
A2	c	d	R2
合計	C1	C2	N

　↑2×2分割表

・仮説の設定
帰無仮説(H₀)：「行・列の度数配置に差がない」と仮定する。
対立仮説(H₁)：「行・列の度数配置に差がある」と仮定する。

・確率を求める
2×2分割表では、期待度数と観測度数の偏りを下の式によって表すことができる。

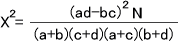
2×2分割表は自由度1のX²分布に従うので、X²分布表より自由度1のX²_αを求める。

・判定
X²≦X²_αのとき、P≧αとなり帰無仮説を棄却できない。
X²＞X²_αのとき、P＜αとなり帰無仮説を棄却する。有意差あり。

………………………………………………………………………………………………………………

　例題
抗がん剤Aを投与したとき、効果がある患者と効果のない患者がいることが分かった。さらに、それには遺伝子のある部分がZ型であるかどうかが疑われている。そこで、抗がん剤Aの効果のあるなしとその患者の遺伝子がZ型であるかどうかを調べた。抗がん剤Aが効くか効かないかに遺伝子Zが関わっているかどうかを検定しなさい。

	通常型	Z型
効果なし	24	56	80
効果あり	49	31	80
	73	87	160

(注：このデータは便宜的に作ったもので、実際のデータではない)

帰無仮説(H₀)：遺伝子Zの有無は、抗がん剤Aの効果に関係ない(互いに独立)
対立仮説(H₁)：遺伝子Zの有無は、抗がん剤Aの効果に関係ある

・計算
計算は、ただ公式に数値を当てはめてX²値を求めるだけである。

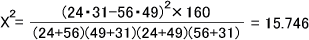
自由度は1なので、X²分布表よりX²_0.05＝3.841となる。X²値＝15.746＞3.841＝X²_0.05となるので、P＜0.05となり帰無仮説を棄却し対立仮説を採用する。つまり、「遺伝子Zの有無は、抗がん剤Aの効果に関係ある」ということができる。

………………………………………………………………………………………………………………

　l×m分割表
2×2分割表では行・列が二方向だけであったが、l×m分割表では行・列がそれぞれl個,m個に分割されている。この分布が行・列に依存しているかどうかを検定する。

	B1	…	Bm
A1	O11	…	O1m	R1

Al	Ol1	…	Olm	Rl
	C1		Cm	N

・仮説の設定
帰無仮説(H₀)：「行・列の度数配置に差がない」と仮定する。
対立仮説(H₁)：「行・列の度数配置に差がある」と仮定する。

・確率を求める
l×m分割表は各セルについて観測度数Oと期待度数Eの偏りを計算して、それを全て足すことでX²値を求める。期待度数Eは次の式で求めることができる。

各セルの観測度数Oと期待度数Eの偏り(ずれの程度)は次の式で表すことができる。

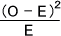
各セルでこの値を計算したら、それを全て足せばよい。

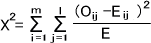
このとき、自由度dfは(l-1)×(m-1)のX²分布に従う。X²分布表からX²_αを求めることができる。

・判定
X²≦X²_αのとき、P≧αとなり帰無仮説を棄却できない。
X²＞X²_αのとき、P＜αとなり帰無仮説を棄却する。有意差あり。

………………………………………………………………………………………………………………

　例題
工場A,B,Cでは製品X,Y,Zを生産している。このとき、一年間に下の表の個数分だけ不良品がでた。工場と製品の種類によって生産される不良品の個数に一定の傾向があるといってよいか。

	製品X	製品Y	製品Z
工場A	32	10	6	48
工場B	27	15	8	50
工場C	30	20	4	54
	89	45	18	152

(注：このデータは便宜的に作ったもので、実際のデータではない)

帰無仮説(H₀)：工場と製品の種類によって生産される不良品の個数は互いに独立(関連性なし)
対立仮説(H₁)：工場と製品の種類によって生産される不良品の個数に関連性あり

・計算
まず、各セルの期待度数Eを求める。

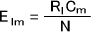
	製品X	製品Y	製品Z
工場A	28	14	5.7
工場B	29	15	5.9
工場C	32	16	6.4

統計量X²値を求めるので、各セルの観測度数Oと期待度数Eの偏りを計算して足す。

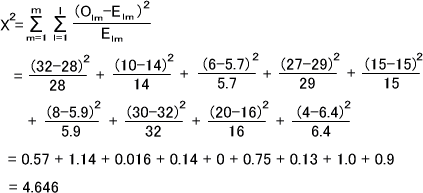
このときの自由度dfは(3-1)×(3-1)＝4である。X²分布表より、自由度4のときのX²_0.05は9.45である。

X²値＝9.45＜13.28＝X²_0.05なので、P＞0.05となり帰無仮説を棄却できない。よって、「工場と製品の種類によって生産される不良品の個数は互いに独立しており、関連性がある」とはいえない。

スポンサードリンク

役に立つ薬の情報～専門薬学｜薬・薬学・専門薬学・薬理学など